A proof of a mathematical statement is a logical argument that
shows the statement is true according to certain accepted
standards.
The idea of proving a statement is true is said to have begun in
about the 5th century BCE in Greece where philosophers developed
a way of convincing each other of the truth of particular
mathematical statements. They had to agree definitions of certain
basic ideas (e.g. point, line, surface), and axioms [see note 1 below ] which were
statements about the starting points (e.g. that it is possible to
draw a circle of any radius). Over time these ideas and many
others were developed in geometrical form, and finally collected
and organised in thirteen Books by Euclid (325-263 BCE) in what
was called his "Elements of Mathematics".
Ideally, the proof of a statement in any particular branch of
mathematics uses the rules, definitions, axioms and theorems of
that branch of mathematics, together with the rules of logic.
Even though arithmetic, algebra and geometry each have different
rules and procedures, we use the same kind of logic for each of
them.
Direct and Indirect Proof.
Direct Proof
Direct Proof is possible if we have agreed axioms and
definitions to start from and an agreed method (a logical
argument) that enables us to proceed logically step by step
from what we know to what we do not know, but think is true.For
example, propositions 5 and 6 in Euclid Book I are about the
equality of the base angles of an isosceles triangle
[see note 2 below ].
This is "obviously" true, but still has to be proved from first
principles.
For some more difficult problems mathematicians developed a
method of "working backwards". This works by assuming that the
desired result is true, and showing that the consequences of
that assumption are consistent with known facts and the basic
principles. The final proof still had to be written out in the
correct order.
Constructive proof is another form of direct proof. This is
where an object has to be directly constructed from the basic
elements of the system. There are many constructive proofs in
Euclid Book I. Proposition 1 for example, shows how to
construct an equilateral triangle [see note 3 below ].
However, it is not always possible to prove something by
keeping to the strict rules of direct proof, and so
mathematicians devised forms of indirect proof to achieve
results.
Indirect Proof
Indirect proof means that we try to find a way of obtaining a
result in some "round about" way. One way is by supposing that
if the result we are looking for is not true, then the starting
point cannot be true. [see
note 4 below ]
Reductio ad Absurdum or Reduction to the Absurd
[
see note 5 below ] is
another method of indirect proof where we try to show the
opposite of the proposition to be true, but as soon as we come
to a situation in the argument that we know is impossible, then
we can say that the original proposition was true.
The proof that the square root of two is not rational
[s
ee note 6 below ] is
a classic problem where an Indirect Proof is used. A proof
originally attributed to Aristotle (384-322 BCE), uses basic
ideas of arithmetic. This proposes that the diagonal of a
square can be represented by a rational fraction, and produces
an argument that constructs a number that is both even and odd
(which is not possible of course).
In the 5th and 6th centuries BCE, the Pythagoreans [see note 7 below ] were interested
in finding a common measure for the side of a square and its
diagonal and discovered that these two lengths were
incommensurable [see note 8
below ] by using a geometrical construction. In
geometrical terms, this can be demonstrated by the successive
subtraction of the smaller length from the larger:
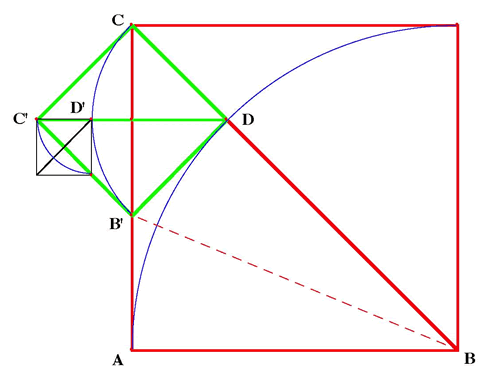
In the red square in Figure I, BD = AB (=AC) and if BC (the
diagonal) and AC (the side) have a common measure it must also
be a common measure for CD = BC-BD.
Now AB' = B'D = DC
And B'C = AC - AB'. So B'C must also have the same common
measure.
So, in the green square, the diagonal B'C and the side DC have
the same common measure. By the same argument as for the red
square, DC' minus DD' leaves D'C' (which again has the same
common measure). This means that no matter what the size of the
square, the common measure will always be the same.
[See note 9 below ]
This is an indirect proof, because it shows that the process
goes on forever producing a lower limit which is zero -
contradicting the idea that a common measure can be found.
 |
|
Diagram I
|
In order to overcome some of the difficulties experienced by the Pythagoreans,
Euclid ( in Book X of his Elements) showed how to manage the mathematics of
incommensurables like
, etc, [See note 10
below ] purely by geometrical constructions.
Keeping to the rules?
However, even in Euclid's Book I, the first proposition about
congruent triangles [See note
11 below ], there were unsubstantiated assumptions.
Euclid used the idea of "superposing" one triangle on another
by a kind of transformation, but there are no postulates or
definitions about what is meant by this action. In other words,
even Euclid used an idea that was not fully justified.
It is now recognised that Archimedes (287-212 BCE) developed
his own methods for calculating difficult results about areas
and volumes enclosed by curves and surfaces, and then rewrote
them in terms of the standard geometrical procedures of the
time [See note 12
below ]. In a letter to a friend he said,
"I set myself the task of communicating to you a certain
geometrical theorem which had not been investigated before but
has now been investigated by me, and which I first discovered
by means of mechanics and then exhibited by means of geometry."
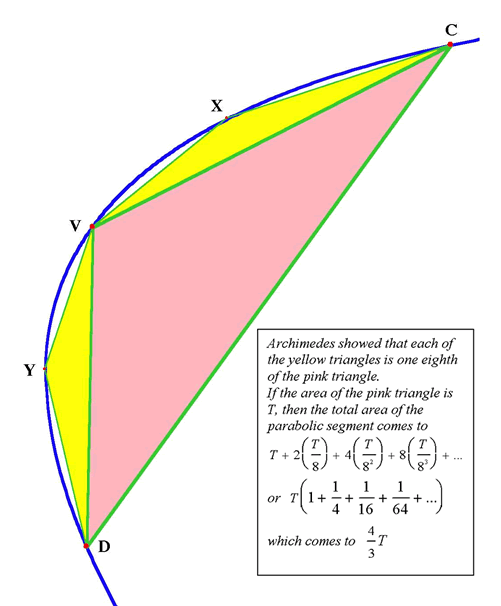
In his first proof of the area of a parabolic segment,
Archimedes used his discovery of the properties of the lever to
balance the weight of a segment of a parabola against the weight of
a triangle. In his second proof he used the method of exhaustion to
show that the area of the segment was
that of the triangle.
So, the ideal proof methods set up by the earliest European
mathematicians were not always adhered to, and later we will see
that other mathematicians were still breaking the rules in order
to achieve new results.
In the early ideas of the calculus, Cavalieri (1598-1647) and
others adapted Archimedes' method of exhaustion to develop the
method of "indivisibles". These were conceived of as infinitely
small elements of lines, surfaces or volumes. Arguing by
analogy, a line was made up of points, a surface was made from
lines, as in the weave of cloth, and a volume thought of as a
pile of very thin sheets of paper. In this way, areas and
volumes of new objects could be compared with areas and volumes
of known objects by a process of transformation.
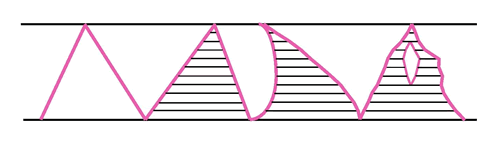
For example, the area of a
triangle was thought of as a very large number of very thin
parallel lines. These were called 'Line Infinitesimals'. Areas
of triangles on the same base and between the same parallels
are equal. If each line remains the same total length, then the
areas of the irregular shapes are the same as the area of the
triangle s.
Throughout the 17th century, "proof by
demonstration" was common.
The general idea was, "If
I show you enough examples of how the algorithm works, then you
will be convinced'.
Mathematicians demonstrated how they achieved their results in
the early calculus by showing diagrams of curves, and
sufficient examples of the procedures to convince their
audience. In most cases the truth of the result was established
by it's practical application, or that it achieved the same
results as already known by a geometrical method. These
experiments and demonstrations aided the discovery of
interesting and important results, but did not conform to the
strict standards of proof because they were based on
unjustified assumptions about the very small quantities
eventually "disappearing".
Many mathematicians were uncomfortable with this situation, but
a logical basis for the calculus methods did not appear until
the middle of the 19th century.
 |
This is part of the first English Edition of Newton's
method for discovering the areas under curves using his
method of infinite series published in 1745.
This is the general rule for what we now call
'integration' in the calculus.
Newton gives
examples to demonstrate how it works with different
algebraic expressions. .
|
When mathematicians like La Hire (1640-1718) and Chasles
(1793-1880) began to develop projective geometry, they used a
method called "projection and section" to show that many
Euclidean proofs were also valid in the new geometry. For
example, it was well known that the ellipse could be obtained
by taking a section through a cone, so why not think of the
ellipse as a transformation of a circle and look for the
properties which remain the same? [See note 13 below ]
 |
 |
For example, making an oblique cut on a circular cone produces
an ellipse. By the method of 'Projection and Section' we can
imagine the ellipse as the 'shadow' of the circle on a plane.
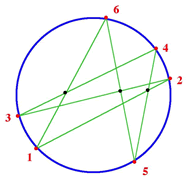
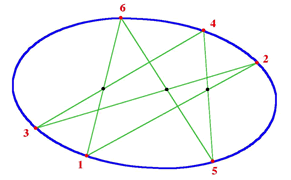
Brianchon's (1783-1864) theorem states that if six vertices of
a hexagon on a circle are joined as in the diagram, the
intersections of the chords joining the points as shown lie in
a straight line. The same result is also true for the ellipse
or any other conic section. This is related to Pascal's theorem
where the three points of intersection of the opposite sides of
a hexagon lie in a straight line.
Imre Lakatos, in his Proofs
and Refutations tells the story of the way the proof of
the Descartes-Euler conjecture (F + V = E + 2) about counting
the Faces, Vertices and Edges of polyhedra [see note 14 below ] was challenged
by scientists working in the new field of crystallography, and
how the original definition of a polyhedron had to be changed
[see note 15 below ].
For example, it is possible to grow isomorphic [see note 16
below] crystals, one 'inside' another and there is a good
argument to suggest that the conjecture might not be valid in
this case. There are many examples where counterexamples of
mathematical propositions have come from the physical world and
mathematicians have had to re-think their theories.
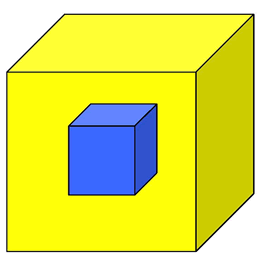 |
The blue cube and the yellow cube are isomorphic.
Can this be one polyhedron or two?
So F + V = E + 4?
What about a tetrahedron inside another tetrahedron?
|
In recent times, computers have been used to investigate
solutions of difficult mathematical problems and one was used
to tackle the proof of the famous Four Colour Theorem using a
program to enumerate all possible maps [see note 17 below ]. The big
question was since all proofs up to this time had been proved
by people, was the fact that it had been completed by a
computer a valid proof or not, and how could anyone be sure the
computer had covered all the possible cases? This kind of
counting procedure is called proof by
enumeration or proof by
exhaustion .
Proof by experiment or
showing examples has always been a problem, as we have seen
with the polyhedra and the maps, since we never know whether we
have all the possibilities or when somebody will discover a
counterexample. We need clear definitions and logical argument
based on agreed facts to provide a sound proof.
Today, mathematicians have many ways of tackling proofs by
using one system to help them find results in another. For
example, Pythagoras' Theorem can be regarded as an arithmetic
relation, an algebraic generalisation, a formula in
trigonometry, or as geometric property. Each of these
approaches gives different insights into the wide range and
application of the general idea.
For this to work, it is
important to be sure that the fundamental properties remain
invariant as we transform the problem from one system to
another.
Wise Men from the East
Recently, important research in ancient Hindu and Chinese
mathematics has uncovered some very different attitudes to
"proving" results. Besides making their own original
contributions, mathematicians wrote Commentaries on the works
of earlier writers to elaborate ideas, to find other ways of
achieving results, and of making new and useful applications.
It is now clear that other cultures have produced ways of
finding "truths" and generalisations quite different from
Aristotle's logic.
Indian Mathematics
Many Indian writers who produced original mathematics, also
took great pains to write commentaries on their own works and
on works of earlier scholars. By the time of Bhaskaracharya
(1114-1185) [see note 18
below ], Indian mathematicians had achieved an
understanding of number systems and solution of equations which
was well ahead of the Europeans. It is in their commentaries
that we find detailed proofs and demonstrations of their
results and discussion of appropriate methods. Until recently,
much of this was obscured by superficial interpretation and
misunderstandings of the cultural context [see note 19 below ].
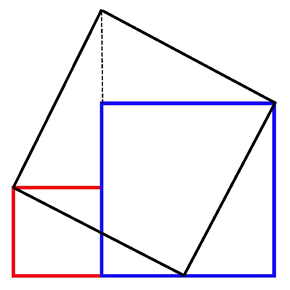 |
An ancient Indian text, the 'Sulbasutra' (meaning
'Rope-Measuring') shows how to use two different size
squares to find the area of a square which is the sum
of the two areas.
By discussing
this diagram, students were able to justify and extend
this method, thus discovering many geometrical
properties much earlier than the Greek
mathematicians .
|
Chinese Mathematics
The most important classic of Chinese mathematics is
The Nine Chapters on the
Mathematical Art which was written some time in the 1st
century CE. Liu Hui (265-316 CE) wrote an important commentary
on this work, and recent research shows us that there are other
methods of investigating mathematical ideas other than the
commonly accepted proof methods of Euclid. During this period
in China, mathematics proceeded as a discussion between master
and student who together focussed on the diagram; its
appearances and possibilities. This shows that deduction from
first principles is not the only model for the discovery and
checking of mathematical results. This is a model of
mathematical reasoning quite different from that of Euclid, but
just as important and fundamental with the aim of
generalisation rather than abstraction, and of deeper
understanding rather than logical proof.
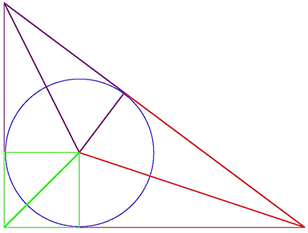 |
This right-angled triangle comes from Lui Hui's
commentary on the 'Nine Chapters'.
By using some simple geometry students were able to
find the area of the triangle and a number of other
relations between the lines and the other areas in the
diagram. This was done quite independently from the
Greek geometers.
|
For pedagogical notes
Use the notes tab at the top of this article or
click here .
Notes
- The Greek word 'axiom' means an agreed starting point.
The word 'postulate' is also used to describe 'what is
possible', or what basic ideas can be used.
- Proposition 5 used to be called the 'Pons Asinorum' (the
Bridge of Asses) because it was once regarded as a test of
understanding for the rest of the Elements.
- This proof has been criticised because Euclid has no
axiom which states that there is a point of intersection when
two lines cross.
- This is often called the contrapositive argument. i.e. If
p implies q, then 'not q' implies 'not p'.
- Some mathematicians choose to call 'reductio ad absurdum'
orproof by contradiction, but others have decided it is a
separate case.
-
A rational number is any one that can be represented by a
fraction, like:
- Pythagoras (c.569-475 BCE) founded a society which
continued well into the 5th century.
- In-commensurable means that there is no common measure
between two given lengths.In this case, a side of a square
and its diagonal cannot be measured exactly in the same
units, or fractions of the unit.
- In this case, a side of a square and its diagonal cannot
be measured exactly in the same units, or fractions of the
unit.
See Pedagogical Notes and Questions 1(c) .
- Another name for these numbers is 'surds'.
- For details on Euclid see D.E. Joyce's commentary at
weblink EUC
- See Netz and Noel (2007) for the most startling recent
discoveries about Archimedes.
- In this kind of projection, the lengths of lines and the
shapes of curves change, but the order in which points are
connected, remains the same.The term invariant refers to properties
that remain the same under some kind of transformation.
- The original conjecture by Descartes was investigated by
Euler in 1758 when attempting to classify polyhedra.
- The publication of Lakatos' original thesis in 1961 was a
major factor in the development of Investigations in school
mathematics.
- Iso-morphic means the 'same shape'. Isomorphic crystals
of chemicals with similar composition can grow on each
another, as often seen in the school science laboratory.
- See Robin Wilson's Four
Colours Suffice (2002). This is the history of the map
colouring problem first proposed by a student of Augustus De
Morgan in 1852. The first proof in 1976 counted 1,936
different maps, but after re-testing the program and
discovering mistakes, by 1994 the number had been reduced to
633. There are still some people who doubt the result.
- Known also as Bhaskara II or 'Bhaskhara the
Teacher'.
- In the early 20th century, Hardy, and others at Cambridge
found many of the results of the brilliant Indian
mathematician Ramanujan (1887-1920) difficult to understand
because the proof methods were unlike anything they had seen
before. Even today, mathematicians are still discovering
important new results from the work of Ramanujan.
References
Berggren, J. L. (2003) Episodes in the Mathematics of
Mediaeval Islam New York, Berlin. Springer (original 1986)
D'Amore, B. (2005) Secondary school students' mathematical
argumentation and Indian Logic (Nyaya).For the Learning of
Mathematics 25 (2) July 2005 (26, 32)
Datta, B. ; Singh, A. N.(1935) History of Hindu mathematics,
a source book. Lahore,: Motilal Banarsi Das. (Reprinted by
Bharatiya Kala Prakashan, Delhi)
Dauben, J.W. (2007) Chinese Mathematics in Katz, V. J. (ed.)
Sourcebook (187-384)
Lakatos, I. (1976) (Eds. Worrall, J. and Zahar, E.) Proofs
and Refutations: The Logic of Mathematical Discovery London.
Cambridge University Press
Kanigel, R. The Man Who Knew Infinity: A Life of the Genius
Ramanujan Johns Hopkins Univerity Press
Katz, V. J. (2007) (ed.) The Mathematics of Egypt,
Mesopotamia, China, India and Islam: A Sourcebook. Princeton
and Oxford. Princeton University Press
Keller, Agathe (2005) Making diagrams speak, in Bhskara I 's
commentary of the Aryabhatiya. Historia Mathematica 32:
275-302.
Keller, Olivier. (2006) Une Archeologie de la Geometrie (An
Archeology of Geometry) Paris. Vuibert
Martzoff, J-C. (1987) A History of Chinese Mathematics
Berlin, New York. Springer
Newton, Isaac. (1745) Sir Isaac Newton's Two Treatises on the
Quadrature of Curves, and Analysis by Equations of an
infinite Number of Terms explained: London John Stewart
Netz, R. and Noel, W (2007) The Archimedes Codex. London.
Weidenfeld & Nicolson
Plofker, K. (2007) Mathematics in India in Katz, V. J.,
Sourcebook (385-514)
Li Yan and Du Shiran (1987) Chinese Mathematics : A Concise
History. John N. Crossley, J.N. and Lun, A.W.C. Oxford.
Oxford Science Publications.
Watson, A. and Mason, J. (1998) Questions and Prompts for
Mathematical Thinking Derby. Association of Teachers of
Mathematics
Wilson, R. (2002) Four Colours Suffice: How the Map Problem
was Solved London. Penguin Books
Web Links
For India and China, there are resources on the French
website:
http://www.dma.ens.fr/culturemath/index.html
. The outstanding scholars here are Agathe Keller for India
and Karine Chemla for China. There is very little from these
two researchers available in English at the moment.
She has also set up a History section on the NCETM website
at:
http://www.ncetm.org.uk/ and
then search for the History of Mathematics Community