What are numbers? Most people, even five year olds, can answer that question to their own satisfaction. Many different answers are given to this question, all more or less acceptable within the discourse taking place. Although negative, fractional and irrational numbers were accepted by scholars in Europe in the sixteenth century, and earlier in ancient civilisations in other parts of the world, until the nineteenth century negative numbers and complex numbers were often disparagingly referred to as absurd numbers and imaginary numbers. These numbers now play an essential part in mathematics, even school mathematics, and schoolchildren learn about them.

Adding and sharing are transactions that we engage in early in our lives and they take us beyond simple counting into the realm of arithmetic. So we should define numbers to be more than labels for naming and recording the size of collections of objects that we have counted. We need to think of numbers as entities that can be combined according to an agreed set of rules which we call arithmetic. The more we know about and use this arithmetic, the more we appreciate that it can be generalised and refined into more and more useful mathematical tools for solving human problems of all sorts.

If we use numbers to describe the size of a collection of objects we need a number for a set that has nothing in it. So we need to expand our concept of number to include zero. While the use of numbers, including place value, dates back at least five thousand years, scholars in Europe were still debating whether zero could be a number as recently as five hundred years ago.

Inverses

Once we have an operation which combines two numbers to give another number, can we undo that process? If we can add 7 what is the operation on the answer which restores it to the original number?

Subtraction is another natural idea based on concrete experience, not of increasing the size of a collection of objects by combining two collections, but of reducing the size of a collection by removing some of the objects. If we have 5 coins and we need 12 to buy something we can ask how many more coins do we need, which number do we add to five to make 12; this is equivalent to finding the answer to 12 - 5, but what number do we add to 13 to make 9 or what is the answer to 9 - 13? If we say that there is no answer to such subtractions then it is only because we do not know about negative numbers. Once negative numbers come onto the scene we have many uses for them.

We can do arithmetic without knowing the mathematical language and nothing so far is beyond the experience of a small child learning to read a thermometer on a wintry day.

We can think of any subtraction as simply the addition of two integers so subtraction is not essential to recording arithmetic operations. For example 9 - 13 = 9 + (-13) = -4. The integer -13 is called the inverse of the +13 because (+13) + (-13) = 0. Every integer has an inverse such that the number added to its inverse gives zero. We are already working with the structure and using the rules which define the arithmetic involved in adding integers. This is an example of a mathematical structure called a group.

From the Natural Numbers to the Integers

Another way to explain the evolution of thinking that extends ideas of counting and addition is to say that if we want to be able to solve all equations of the form a + x = b, where a and b are given and we have to find x, then for all such equations to have solutions we need to work in the set of integers. For example 9 + x = 5 had no solution within the set of counting numbers.

Rational Numbers

In the same way as horizons are extended to include negative numbers it is also everyone's experience to learn that fractions are also numbers. Mathematicians call these numbers rational numbers . Children are interested in 'fair shares' even before they start school so division is also based on concrete experience.

Addition and subtraction are inverse operations inextricably connected. Similarly multiplication and division are inverse operations in the sense that 5 ×4 = 20 and 20 ¸4 = 5.

It is not until we can work with the set of rational numbers that every addition, subtraction, multiplication and division of two numbers in the set gives an answer that is also a number in the set giving a 'self contained' number system. The rules for the arithmetic of rational numbers are simple. This set of rules defines what mathematicians call a field.

(1) The set of rational numbers is closed under addition, and associative, the rational number zero is the additive identity and every rational number has an additive inverse. We say rational numbers form a commutative group under addition.

(2) The set of rational numbers, leaving out the number zero, is closed under multiplication, and associative, the rational number one is the multiplicative identity and every rational number in this set has a multiplictive inverse. We say the rational numbers, leaving out the number zero, form a commutative group under multiplication.

(3) When we add and multiply rational numbers we use the distributive law. For example

3×(4 + 5) = 3 ×4 + 3 ×5 = 27.

We need to extend our ideas of the arithmetic of whole numbers to include fractions (rational numbers) because we cannot solve all equations of the form ax = b, where a, b and x are integers, a and b are given and we have to find x. If a, b and x are rational numbers then all such equations have solutions.

Irrational Numbers

Many people use only rational numbers because, even though no rational number will give exact measurements of even simple shapes, exact measurements can be approximated to a high degree of accuracy by rational numbers. The length of the diagonal of a unit square is Ö2 and this is an irrational number, one that cannot be written as the quotient of two integers. It is approximately 1.414 but it cannot be given exactly however many decimal places we use. See the interactive proof sorter for the proof that

Real Numbers

The rational and irrational numbers together make up the real numbers. Each real number corresponds to exactly one point on a line and all the points on that line are represented by real numbers. We call this line the real line. The real numbers are equivalent to one dimensional vectors and, together with addition and multiplication, form a field. We have now discussed two different examples of fields of numbers, the rationals and the reals.

Complex Numbers

In the field of real numbers we can solve the equation x² = a only when a is positive but not when a is negative. Real numbers are good enough for many mathematical purposes but clearly they have limitations. It is necessary to recognise the existence of two dimensional numbers, the complex numbers, in order to solve all quadratic equations. See

What else can we do with complex numbers? Complex numbers are two dimensional; whereas real numbers correspond to points on a line, complex numbers correspond to points in the plane. The complex number written as x+yi corresponds to the point in the plane with coordinates (x,y). Let us examine the significance of this mysterious i referred to as an 'imaginary' number. What role does it play?

Complex Numbers and Rotations

Think about taking a real number and finding its additive inverse, say 5 and -5. To move from any real number to its additive inverse we must multiply by -1, or to think of it another way, we must move from the positive real axis to the negative real axis, a half turn about the origin so the point (5, 0) moves to (-5,0), that is the complex number 5+ [0×i] moves to -5+[0×i]. No obvious clue there as to the role of i but let's probe a bit further and think more about rotations. Two quarter turns make a half turn so what happens when we rotate the plane by a quarter turn about the origin? The point (5, 0) moves to (0,5), that is the complex number 5 + [0×i] moves to the complex number 0 + 5 i which appears to be equivalent to multiplying by i, that is i(5 + [0×i] ) = 0 + 5i. (It is not necessary to write in [0×i] here but we do so to make clear how the mappings of the complex numbers correspond to the mappings of the points in the plane including the points on the real line which correspond to real numbers.)

We have seen that a real number is mapped to its additive inverse by multiplying by -1. So if a quarter turn of the complex plane is equivalent to multiplying by i then a half turn (that is two quarter turns) must be equivalent to multiplying by i twice which must be the same as multiplying by -1 and this tells us that i² = -1. Taking i² = -1 this fits in with moving (5, 0) to (-5, 0), or correspondingly, 5 + [0×i] to i²(5 + [0×i]) = -5 + [0×i]. A quarter turn moves (0,5) to (-5,0) or equivalently 0 + 5i to -5+ [0×i] and this time multiplying by i gives i(0 + 5 i) = 5i² + [0×i] = -5 + [0×i].

All this works beautifully because i² = -1. This little complex number, corresponding to the point (0,1), not only allows all polynomial equations to have solutions but gives a powerful tool for working with rotations. In the form x+yi complex numbers can be added, subtracted, multiplied and divided according the the same rules as elementary arithmetic, that is the complex numbers form a field. We now have three fields of numbers, the complex numbers, the reals and the rationals.

Another glimpse of the beauty of complex numbers is seen in the formula

eiq=cosq+ isinq

linking geometry, trigonometry and analysis. This formula involves the important real number e as well as the complex number i. Students usually meet this formula and use it in their last year in school if they are preparing to study mathematics, physics or engineering in higher education. In this formula the angle q is given in radians and not in degrees but the conversion is a simple matter because p radians is 180^o. If we put q = p we have the very beautiful result

eip = cosp+ isinp

which connects the important numbers e, i, p and -1 in the simple little formula

eip = -1.

If we put

q =

p 2

we have

ei[(p)/2] = cos p 2 + isin p 2 = i

which suggests that multiplying by

eiq=cosq+ isinq

might be equivalent to rotating the complex plane by an angle q ( as this works for quarter turns and i) and this is indeed the case.

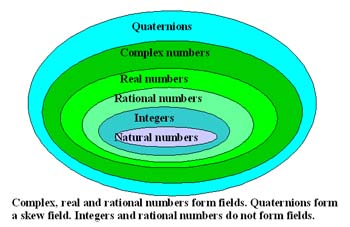If one dimensional real numbers can be generalised to two dimensional complex numbers and both systems form fields, the obvious question is "what about higher dimensional numbers?"

Three dimensional numbers do not exist

Three dimensional vectors are of fundamental importance in applied mathematics. They can be added and subtracted but although there are two different types of vector multiplication, multiplicative inverses do not exist and so the set of three dimensional vectors do not form a field and cannot be a set of numbers. To understand the significance of the two alternative definitions of vector multiplication it is necessary to know about four dimensional quaternions.

Quaternions

If we think about rotations of the plane, and i as the key to understanding the essence of complex numbers, what about rotations of 3 dimensional space? For rotations of the plane that map the plane to itself there is only one possible axis of rotation which must be perpendicular to the plane. [Without loss of generality we can take the centre of rotation to be at the origin.] However in 3 dimensional space there are infinitely many possible axes of rotation through the origin. If we want to specify an axis of rotation we need the three coordinates for one other point on the axis. Whereas in the complex plane we only need one parameter to specify a rotation (the angle of rotation), in 3 dimensional space we need four parameters (three to specify the axis of rotation and one to specify the angle of rotation). This takes us to four dimensions and explains why there are two and four dimensional numbers, but not three dimensional numbers, and why quaternions provide a very efficient way to work with rotations of 3 dimensional space.

Quaternions, discovered by the Irish mathematician Sir William Rowan Hamilton in 1843, have all the properties of a field except that multiplication is not commutative. Moreover quaternions incorporate three dimensional vectors and much of vector algebra and provide simple equations for reflections and rotations in three dimensional space.

As applied mathematics and physics regularly deal with motion in space, quaternions are very useful. It is a quirk of history that this was not perhaps fully appreciated at first and vector algebra was invented as a tool to work with motion in 3 dimensional space and concentrate attention on only 3 dimensions. However a lot of the simplicity of the equations involving quaternions was lost as well as sight of the underlying reasons for defining scalar and vector multiplication in the way they are defined. Nowadays quaternions have come into their own again as an important tool frequently used in applied mathematics and theoretical physics. Quaternions are also now widely used in programming computer graphics because the quaternion algebra involved in transformations in 3 dimensions is so simple.

Higher Dimensional Numbers

What about higher dimensional numbers? Number theorists work with Clifford Algebras, named after William Clifford (1845-1879), which generalise complex numbers and quaternions to dimensions 2, 4, 8, 16... and higher dimensions (all powers of 2). Some of the properties of a field are lost, for example quaternions are not commutative under multiplication, but Clifford algebras are associative. Clifford algebras have important applications in a variety of areas including geometry and theoretical physics. Other generalisations are studied for which multiplication is not associative.

This 'big picture' discourse has ranged, without getting too technical, from kindergarten mathematics to the fringe of research into analysis and applications of number. There is a wealth of literature to take the reader further at every level and the links below may provide a useful start on such a journey of discovery.