All too often we ignore the creative aspects of mathematics in our classroom teaching, and focus on routine exercises and the repetition of procedures. In doing so we are unlikely to spark enthusiastic responses to the subject from the children. Not many children say that maths is their favourite lesson and yet it could be so easily.

On the NRICH website there are many ideas for making connections between mathematics and other subjects, as well as links to other valuable resources on the Internet. Mathematics is often described as the study of pattern, which might help to explain its strong connections with art, leading to some of the most creative aspects of mathematics. Let us consider tessellations as just one aspect of pattern. Let's start by looking at tessellating equilateral triangles and then go on to look at various other kinds of triangles and then quadrilaterals.

Tessellating triangles

The web-page version of the following investigation can be found here .
Equilateral triangles have three sides the same length and three angles the same. Can you make them fit together to cover a sheet of paper without any gaps between them? This is called "tessellating".
What about triangles with two equal sides? These are isosceles triangles. Can you tessellate all isosceles triangles? How do you know?
Now try with right angled triangles. These have one right angle or 90 degree angle.
Some triangles have sides that are all different. Can you tessellate these?
Could you tessellate any triangle?
What about squares? Rectangles? Kites? Any other polygons with four sides?
You could try polygons with more than four sides. What do you find?

There is a range of resources that you can use to explore such ideas, such as Polydron or ATM mats -playing around with shapes that you can move is satisfying and productive but some children become frustrated that they don't have a record of their results. You could use a digital camera to record (and make a diplay) or ask the children to transfer their ideas onto paper, perhaps using cardboard templates.

Whenever I think of tessellations I always think of Escher, an artist who has certainly explored this area thoroughly. It is indeed questionable whether he was more of an artist or more of a mathematician. Exploring how his tessellations link to underlying repetitions of quadrilaterals with "bits" cut out and added on gives children a creative way into developing their own more elaborate tessellating patterns. It might be worth avoiding the more sinister patterns though! Websites presenting Escher's work abound and can easily be found through search engines. The official website is a good place to start: www.mcescher.com.

Penrose tilings

One living mathematician who has done a lot of work in this area is Roger Penrose. He has explored tiling patterns that cover the whole plain like a tessellation but are not regular in the way in which the pattern repeats itself. His designs are stunning in their beauty and underlying simplicity, and we have developed one of them into an interactive activity called "Building Stars ".


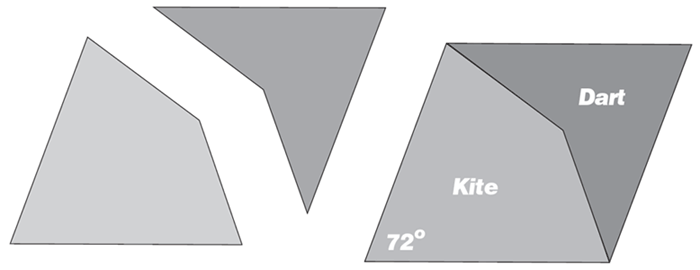
This design uses two quadrilateral shapes -a kite and a dart -and they are repeated over and over again but do not fit together in a regular way. As well as exploring this pattern interactively on the website you could also use the templates to create your own kites and darts either cut out in sticky paper or in sponge so that you could print a pattern using the shapes.

One of the key features of the kites and darts that are used in this pattern is the ratio between the lengths of the sides, which is the Golden Ratio. Investigating the importance of this number in art and architecture as well as more mundane things like the shape of A4 sheets of paper is yet another fruitful avenue of mathematical study and once again it links to many different curriculum areas.


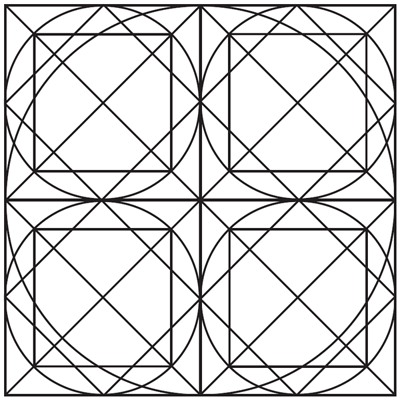
The mention of architecture takes us into Islamic art, of which decorative patterns are a central feature owing to the prohibition of representation of natural forms in Islam. As is often the case with constraints of one kind or another, this restriction has led Islamic artists to become masters of abstract geometrical patterns and tilings. One frequently used tiling is a stars and crosses design which can be constructed using a ruler and a pair of compasses.

The template, below, can also be found here in the form of an interactive game to play with the pattern. Constructing the pattern oneself is quite a challenge even for the highest attainers.


Spirals

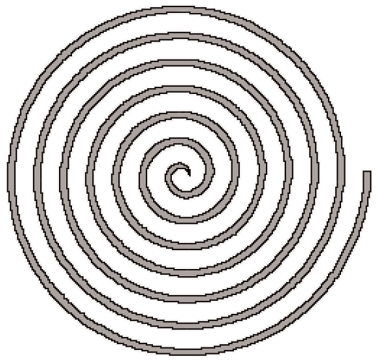
Another kind of pattern that is found in art and that has mathematical significance is the spiral. In fact, there are many different spirals and they arise out of different contexts. Archimedes, the Greek mathematician, has one named after him which can be constructed using a cotton reel, strip of paper and a pencil and looks like the pattern below: it is the path followed by an object travelling away from a given point at constant velocity.


Of course there are also spirals all around us - from screws to the pattern of segments in a pineapple, or the way leaves are spiralled round the stem of a plant. Did you even make twizzlers as a child? Draw a spiral on each side of a circular piece of card, make two holes either side of the centre and thread a length of string through them. Tie it to make a loop, keeping the card in the middle, twist both ends and then pull. The twizzler will work and you can experiment to see what visual effects can be made. Make links to colour mixing too, by colouring the spirals in different colours.

Teddy Town

What other connections can we make with mathematics across the curriculum? One approach to teaching maths that I and many others find useful is to contextualise it within a story, and there are many stories that we can tell that have mathematics in them. One of my favourites is a story about "Teddy Town " where different bears of different colours live in different streets. It offers a context for an interesting problem about shape, space and combinations.

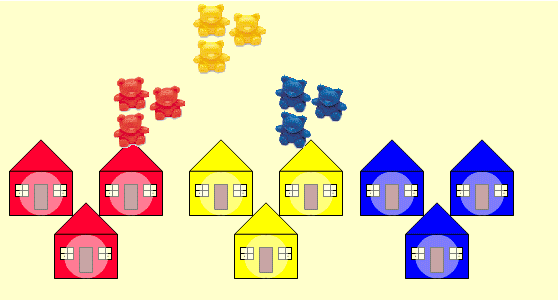
In Teddy Town, teddies are either red, yellow or blue and they live in red, yellow or blue houses. There are nine teddies - three red, three yellow, three blue - and nine houses - three red, three yellow and three blue.

What are the nine different combinations of teddies and houses?


Here is a map showing Teddy Town:



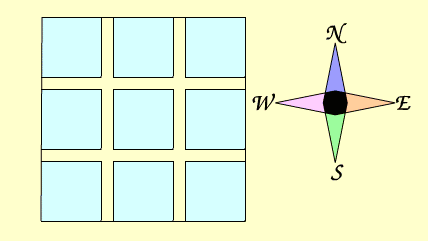
The streets are very special. If you walk along a street from east to west, or west to east, all the houses are a different pattern and the teddies living in the houses are a different pattern too. The same is true if you walk along the streets in a north-south or south-north direction.

In other words, looking at the map grid, each row and column must have different patterned houses and different patterned teddies.

Can you arrange the nine different combinations you've found on the map grid?

There are plenty of other stories that you may be familiar with that have mathematics in them. For example, Eric Carle's picture books such as The Very Hungry Caterpillar and The Bad Tempered Ladybird , which can help to introduce young children to counting and the concept of time on the clock. For older children, Hans Ensenberger's The Number Devil is a delightful story that describes a young boy dreaming about numbers which he is introduced to by the Number Devil. It includes all sorts of different numbers from Fibonacci numbers to triangle numbers and prime numbers, with a chapter on each. Wouldn't it be refreshing to have a shared reading of a mathematics book for a change?

A couple of years ago I was involved in a project in Lewisham in which I worked with an expert Theatre in Education team called Make Believe Arts to develop some mathematical stories that had maths built into them as part of the story itself. The children acted out the stories and in each case a particular mathematical problem had to be resolved in order for the story to progress. It was tremendous fun and proved a memorable experience for the children. A traditional story that is similar is an Indian tale called Sissa's Reward :

According to an old Indian myth, Sissa ben Dahir was a courtier for a king. Sissa worked very hard and invented a game which was played on a board, similar to chess. The king decided to reward Sissa for his dedication and asked what he would like. Sissa thought carefully and then said, "I would like one grain of rice to be put on the first square of my board, two on the second square, four on the third square, eight on the fourth and so on." The king thought this was a silly request, but little did he know...

Left is a chess board with the first few squares filled with grains of rice as Sissa asked for.


Egyptian maths

I have already mentioned quite a few mathematicians of historical significance and the connections between maths and history are very strong and well worth investigating. There is the history of mathematics itself, which is fascinating in its own right. It is hard to imagine how the Romans did arithmetic when one looks at their number system, and the development of our own conventions are fascinating. How did they manage without a symbol for zero for so long? Delving back into ancient history, the Egyptians were brilliant at geometry and their methods helped them to construct the Pyramids, but what about fractions? They had an interesting method which only allowed them to express fractions as unit fractions with one as the numerator. Expressing fractions as the sum of unit fractions is tricky but is an interesting mathematical problem:

This problem can be found on the website here .
Did you know that the Egyptians wrote all their fractions using what we call unit fractions? A unit fraction has 1 as its numerator (top number). Here are some examples:

1/5     1/3     1/2

They expressed all fractions as the sum of unit fractions, but they weren't allowed to repeat the same unit fraction in the addition. So we couldn't write:

3/8=1/8+1/8+1/8

because we've used 1/8 three times. However, this would be fine:

3/8=1/4+1/8

How could the Egyptians write 3/4? Are there any other ways?

What is 2/3 written as the sum of unit fractions? Again, investigate different ways of doing this.

Find some more fractions (say three or four) which you can write as the sum of unit fractions.

Fibonacci

What about the great mathematicians? I have already mentioned Archimedes but there are so many others: Pythagoras, Escher, Euler and of course Fibonacci. St Andrew's University in Scotland has a website dedicated to the history of mathematics and it is possible to find a different mathematician for every day of the year there. There are a number of sources of information on the web about Fibonacci but one of the best must be that developed by an enthusiast, Ron Knott . He offers enough ideas to fill your maths lessons for weeks as well as your history, science and art lessons! There are lesson ideas, challenging questions and links to other websites galore. Here is a sample:

Fibonacci's Rabbits
The original problem that Fibonacci investigated (in the year 1202) was about how fast rabbits could breed in ideal circumstances.

Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was:

How many pairs will there be in one year?

  1. At the end of the first month, they mate, but there is still only one pair.
  2. At the end of the second month the female produces a new pair, so now there are two pairs of rabbits in the field.
  3. At the end of the third month, the original female produces a second pair, making three pairs in all in the field.
  4. At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produces her first pair also, making five pairs.
The number of pairs of rabbits in the field at the start of each month is 1, 1, 2, 3, 5, 8, 13, 21, 34...

Can you see how the series is formed and how it continues?

The Fibonacci connection brings me more or less to the end of this article, although I have only scratched the surface of the possibilities for linking maths with other curriculum areas in exciting and challenging ways. I haven't even mentioned geography, with maps, bearings, contours just as starters, or physics, where we could explore speed, time, rates of change, measurement and a host of other things. I will leave those for another time. The creative possibilities are endless and are a fruitful field for exploring.

Bibliography

Carle, Eric (1982) The Bad-Tempered Ladybird . Picture Puffins, London. ISBN 0140503986
Carle, Eric (1970) The Very Hungry Caterpillar . Hamish Hamilton, London. ISBN 024101798X Enzensberger, Hans Magnus (2000) The Number Devil: A Mathematical Adventure . Henry Holt & Company. ISBN 0805062998

This article first appeared in Maths Coordinator's File issue 19, published by pfp publishing. To find out how to subscribe to the Maths Coordinator's File, click here .