Complex numbers can be a difficult topic to break into. Understanding them often involves accepting what may seem to be arbitrary rules about a meaningless idea. Only later do the rules make sense and the meaning, applications and connections to other areas of Maths and Physics become obvious.

The aim of the "Arrow Arithmetic" and "Twizzles" exercises is to introduce complex numbers in a new way - as an extension of real numbers, following on from them more naturally than in the conventional approach.

Exploring the Number Line

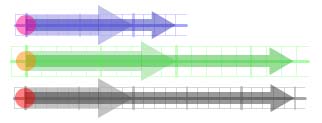
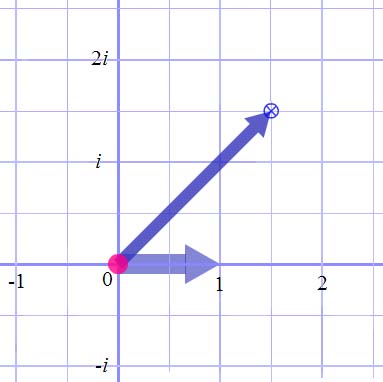
Instead of plunging straight into complex numbers, the problems begin by taking a fresh look at real numbers - numbers on the number line - and their arithmetic. Numbers are represented by a pair of arrows - one wider and one narrower - described as twizzles. The wider arrow is the unit arrow which defines the scale. The value of the twizzle is given by the length of the narrower number arrow and its direction - in the same direction as the unit arrow for positive numbers and in the opposite direction for negative numbers. For example, the twizzle below represents the number two because its number arrow is twice as long as its unit arrow and points in the same direction.

Figure 1

The interactive animations allow you to manipulate the arrows by changing their values, moving them around the screen, stretching them and separating the unit from the number arrows. To get a handle on their behaviour you could also make real-life twizzles to manipulate, using strips of elastic band. Each strip needs three marks on it: one for the origin (the pink spot in the diagram above), one for the head of the unit arrow and the third for the head of the number arrow. You can try the Arrow Arithmethic exercises using elastic twizzles as well as the virtual ones in the animations.

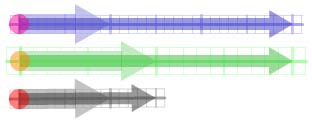
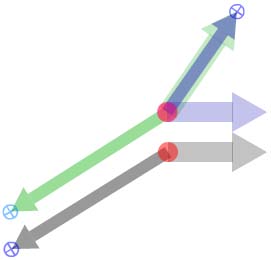
Twizzles can be used to do arithmetic geometrically, with arrows representing steps along the number line. The simplest example is addition. To add twizzles, they are first scaled so that their unit arrows all have the same length and direction. The number arrows are then arranged nose-to-tail. The twizzle representing the sum has a unit arrow of the same size and direction as the original unit arrows and and a number arrow streching from the tail of the first number arrow to the head of the last. In Figure 2, the blue and green number arrows have been added together to give the grey. Below the number arrows are the unit arrows, lined up to show their matching size and direction.

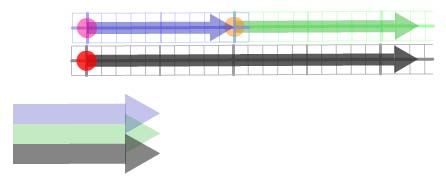
Figure 2

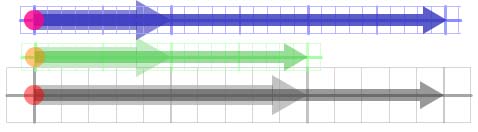
In Figure 3, the green twizzle has been subtracted from the blue one to give the grey. Because subtraction is just addition of a negative number, the rule for twizzle subtraction is similar to addition, except that we must start by rotating the green twizzle through 180⁰ to make it negative relative to the blue unit arrow. The twizzles are then added nose-to-tail as before.

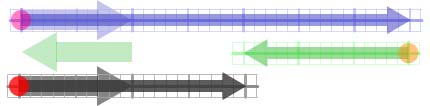
Figure 3

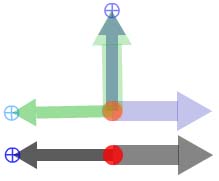
Multiplication is a little different. Figure 4 shows an example, where the blue and green twizzles are multiplied to give the grey twizzle. First we adjust the length and direction of the green unit arrow until they are the same as those of the blue number arrow. The other two arrows (the unit arrow from the blue twizzle and the number arrow from the green) make up the grey twizzle representing the product. We could have got the same answer by matching the lengths of the blue unit arrow and the green number arrow, in which case the product would have been represented by the remaining two arrows.

Figure 4

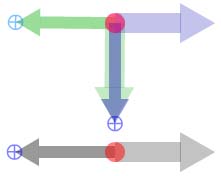
Dividing by a number means multiplying by its reciprocal (one divided by the number), and to find the reciprocal of a twizzle you swap the lengths of its arrows. So Figure 5a shows how the blue twizzle is divided by the green: the roles of the arrows in the green twizzle have been exchanged so this time we match the sizes of the number arrows and the two unit arrows make up the twizzle for the answer. Because we matched the number arrows, the unit arrow of the blue twizzle becomes the unit arrow in the result and the unit arrow of the green twizzle becomes the number arrow in the result. We could also have got the answer by matching the unit arrows (Figure 5b), but we would have had to take the green number arrow for the grey unit arrow and the blue number arrow for the grey number arrow.

Figure 5a

Figure 5b

New Directions

The twizzles we have looked at so far have arrows pointing in the same or in opposite directions and can represent any number on the number line. What about twizzles whose arrows point in completely different directions? These represent numbers not on the number line - complex numbers. Twizzles can be used to think about what complex numbers are and how they behave.

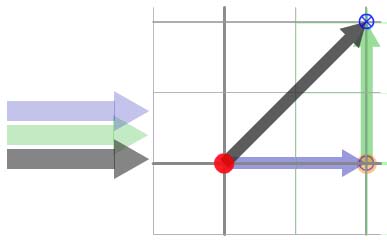
Let's add two twizzles. In the diagram below, the blue twizzle has its arrows parallel in the way we've met before. It represents the number 1. The green twizzle has its arrows at 90⁰and length 1 so that following the number arrow would not move us along the number line at all but one unit at right angles to it. The sum of the blue and green twizzles (the grey twizzle) can be constructed using the rule for twizzle addition. As shown, it turns out to have length Ö2 (using Pythagoras) and be orientated at 45⁰ to the unit arrows.

Figure 6

Now a multiplication. In Figure 7, the blue and green arrows have been multiplied together as before, by matching the lengths and directions of one unit arrow and one number arrow. The grey twizzle gives the result: a unit arrow from the blue twizzle and a number arrow from the green one. The size of the grey twizzle (the length of its number arrow in units of its unit arrow) is the product of the values of the green and blue twizzles. The angle between its arrows is the angle of the blue twizzle plus the angle of the green twizzle (measuring all angles anti-clockwise from unit to number arrow).

Figure 7

Getting More Complex

How should we describe the numbers whose twizzle arrows point in different directions? Conventionally, we start by arranging them on a diagram called an Argand diagram, like the one in Figure 8. The tails of both twizzle arrows are placed at the origin, and the twizzle is adjusted so that the head of the unit arrow is at one on the horizontal axis. The head of the number arrow now indicates a point which represents the twizzle on the diagram.Figure 8 shows how the number 1.5+1.5i is represented.

Figure 8

Numbers on the number line have twizzles whose arrows both point in the same direction, so these all sit on the horizontal axis in the Argand diagram. These numbers are called real numbers and the horizontal axis, which is really just the number line, and is called the real axis. Numbers sitting on the vertical axis aren't real, so instead of labelling it with the real numbers we label it i, 2i, 3i, etc. where i, which stands for imaginary, tells us that these numbers are on the vertical, imaginary axis instead of the number line. So a point on the positive vertical axis one unit from the origin represents a number called i whose twizzle is two arrows of equal length pointing at 90⁰ to each other, measuring anti-clockwise from unit to number arrow.

What is the number i? We use twizzles to multiply i by itself. The blue and green twizzles both represent i, and the grey twizzle is their product.

Figure 9

So i²=-1, or in other words, i is a square root of -1. From our experience of the real numbers, numbers have two square roots. So what is the other root of -1? What other twizzle can be multiplied by itself to give -1?

Figure 10

The numbers i and -i are the square roots of -1. And in the same way, 2i and -2i are the roots of -4, 3i and -3i are the roots of -9, and so on.

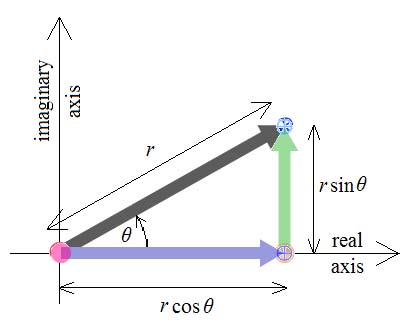
What complex number does an arbitrary twizzle represent? Take a twizzle whose length is r times the length of its unit arrow, with an angle q between its arrows. We can construct any twizzle from the sum of a purely real number, a, and a purely imaginary one, b ×i, as shown (Figure 11). The blue arrow has lengtha and the green arrow has length b. Basic trigonometry gives the sizes of these real and imaginary numbers and we can write our complex number, z, as:

z = a + bi = r(cos q+ i sin q)

Figure 11

A complex number can be described in two ways: by the purely real and imaginary numbers a and bi of which it is the sum, or by its modulus (length), r, and argument (angle to the real axis), q. It turns out that (cos q+ i sin q) is equal to e^{i q} as long as q is in radians, not degrees. So another way of writing the number represented by our arbitrary twizzle would be z = re^{i q}.

When adding and subtracting complex numbers, the a+bi form is helpful because we can add or subtract the real parts of the two numbers separately from the imaginary parts. For example,

(a+bi) + (c-di) = (a+c) + (b-d)i

This makes sense when we think of the twizzles on the Argand diagram. The distance by which the ''sum'' twizzle moves us along an axis is the sum of the distances each twizzle would move us on its own.

For multiplying complex numbers, the re^{i q} form is more helpful because we can deal with the size and direction parts of the twizzles separately. For example,

re^{i q}×se^{i f} = (rs)e^i(q+f)

This makes sense because, as we saw in Figure 7, the length of a product twizzle is the product of the lengths of the factor twizzles and the angle is the sum of the angles. To divide complex numbers, you would divide the moduli and subtract the arguments.

Complex Numbers Reach Places other Numbers don't Reach

Think about the equation x²-2x+10 = 0. Using the formula for solving quadratic equations gives us the solutions

x = 1± __
Ö-9

Before we knew about complex numbers, we might have said that the equation had no roots, but now we know that this is not true. It has no real roots, but it does have two complex roots, at x = 1+3i and x = 1-3i. Complex numbers have allowed us to answer a previously unanswerable question.

Now try x³ = -1. The real numbers give us one solution: x = -1. But what if we use the re^{i q} notation? The modulus of -1 is 1, and we can say that the argument is pradians (180⁰), but if the argument were 3 p, 5 p, 7 p and so on, the twizzle would still look the same. Adding 2p radians to the argument of a complex number leaves it unchanged. So, writing the equation again, expressing x as re^iq,

r³e^3iq = e^ip = e^3ip = e^5ip = e^7ip = etc.

and the solutions are r = 1 with q = p/3, p, 5p/3, 7p/3, etc . Discarding the ones which are the same as others by the ''adding-2p'' rule leaves three solutions:

x = e^{i p/3} x = e^{i p} x = e^5ip/3

The second of these is -1, which we already knew about, but the other two are both complex. Once again, complex numbers have provided solutions we never knew existed.

We have just uncovered a whole extra world of numbers. Might there be any more? In fact, you can find all the roots of any polynomial equation using just the complex numbers, a result known as the Fundamental Theorem of Algebra.

Why Complex Numbers?

You can't have i apples in a basket, or take £(7+5i) out of a cash machine, or travel at

_____
Ö-5000

miles per hour, so why bother with complex numbers? Are they just an intriguing mathematical phenomenon with no practical meaning or use? The answer, of course, is no: complex numbers are essential in Physics as the tools for describing oscillating quantities: atoms vibrating in their molecules, the swing of a pendulum or light waves travelling through space. Complex numbers can also be used to think about geomety on a flat piece of paper because they correspond to points on the Argand diagram. A famous example is the Mandlebrot set (Figure 12). The well-known image is in fact an Argand diagram, where the points coloured black correspond to the complex numbers c for which the series z_n+1 = z_n² + c doesn't tend to infinity.

Figure 12

Transformations of points are equivalent to operations on complex numbers. For example, translating a point a units in the x-direction and b units in the y-direction means adding (a+bi), and rotating 90⁰ anticlockwise about the origin corresponds to multiplying by i (to see this, think of doing the arithmetic using twizzles). There are much more complicated transformations, too, with all sorts of interesting properties, and applications from drawing the field lines from an electric charge to pinpointing the source of an earthquake based on measurements made all round the globe.

Some Further Reading

For more information on topics skimmed over here, try these:

For an intuitive proof of the fundamental theorem of algebra without lots of mathematical jargon and notation, see p38 of A Mathematical Bridge by Stephen Hewson, published by World Scientific.
Plex and Plex2 let you experiment with graphical representations of functions of complex numbers.
One of the geometrical transformations you can perform using complex numbers, which is used for locating earthquakes, is a stereographic projection. There's an animation, and some description in words here .
NRICH has two other articles on Complex numbers. What are Complex Numbers? gives a sense of where complex numbers fit into the bigger picture by bringing in related topics, such as trigonometry, exponential functions and vectors. It also proves that the exponential and trigonometric expressions for a complex number are equivalent. An Introduction to Complex Numbers goes into more mathematical detail, and includes exercises.
There's lots on the internet about the Mandlebrot set, which you can easily find using Google. Wikipedia has some particularly beautiful pictures. There's an applet for exploring the Mandlebrot set here , with a link to some explanation .