Probability is a big deal. Why? Because it's the mathematical way of thinking about risk. Get risk right and you could make millions on the stock market, but get it wrong and you could send innocent people to jail.

The trouble is that our brains haven't evolved to let us assess risk consistently, realistically and reliably, so our intuition - our "feel" for the situation - is very often wrong. But that means that understanding probability can be incredibly powerful because it tells us things our intuition can't, or doesn't. It can lead to some startling conclusions and tell us things we never even knew we could work out.

One very useful tool for thinking about probability is Bayes' Theorem. Its power comes from the fact that it lets us do probability problems backwards: you might be used to predicting results based on something you know about ("There are six pictures on this cylinder and I win when I get the £ sign. What's the probability of me winning next time?"), but Bayes' theorem tells you things about the world based on your results ("In the last 12 tries I haven't scored any £ signs. Is the machine fixed against me?").

There's a well known problem in probability called the Monty Hall problem, which illustrates (part of) what Bayes' theorem can do. It goes something like this:

You've reached the final round in a TV game show. In front of you are three shiny red doors labelled in gold: A, B and C. Behind one of the doors, you are told, is a car (or a holiday, or £1000, or a cuddly toy, or whatever the prize might be in your fantasy game show). Behind each of the other two doors is a dustbin. The rules are that you have to choose a door, and you'll win whatever is behind it. Being a logically minded person with a good training in probability, you realise that you have an equal chance of winning, whichever door you choose. So you choose door A because it is first on the list.

The game show host stands beside the closed doors, the sequins on his jacket glinting in the studiolights."You've chosen door A." he says. "Is that your final answer? "
"Yes." you reply.
He addresses the audience: "Our contestant has chosen door A. Now, according to the rules of the game, I'm going to open a different door to the chosen one, to reveal one of the dustbins," and he pulls open door B to reveal, as promised, a rubbish bin. Turning back to you he explains, "This is the last chance you will have to change your mind. Door B wins you a dustbin. Would you like to stick with your choice, door A, or switch to door C?"

The spotlight turns on you. The tension-building music begins to play. The remaining two doors are giving nothing away as you try frantically to make a decision.

What should you do?

Back to Bayes-ics

Leaving the TV studio behind for a while, let's think about probability, and in particular about the unremarkable-looking formula we call Bayes' theorem. Bayes' theorem isn't the only approach to this problem, and you might be interested to think about some other ways of tackling it, but it does provide a neat, efficient solution, and gives some interesting insight.

You may well have come across Bayes' theorem before. If not, though, it's straightforward to derive. Think about two events, which can each have two outcomes: either it's raining or it's not, and either my bus is late or it's not. We'll call the case where it's raining R, and the case where the bus is late L. The probabilities of the various combinations of events can be shown on a Venn diagram.

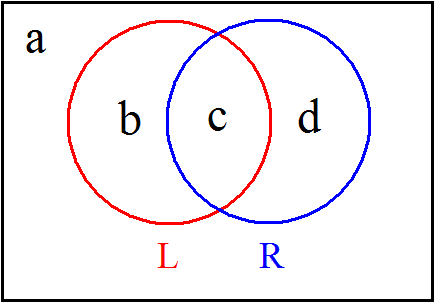
I'm going to write the probability of event X as

P (X)

, so the diagram is saying that

P (L) = b + c and P (R) = c + d

I'll write the probability that it's raining and the bus is late as

P (R \cap L)

, so

P (R \cap L) = c

Bayes' Theorem is about conditional probabilities - that's quantities like "the probability that my bus is late, given that it's raining". We know that it's raining - that we're in the blue circle - so the probability that the bus is late too is

P (L | R) = \frac{c}{c + d} = \frac{P (R \cap L)}{P (R)}

(1)

I've used

P (L | R)

to mean "the probability of L happening, given that R does".

By the same logic, if the bus is late then the probability that it's also raining is

$P (R | L) = \frac{c}{b + c} = \frac{P (R \cap L)}{P (L)}$ $(2)$

So what? Well, because the quantity $P (R \cap L)$ appears in both equations (1) and (2), we can rearrange them to give

$P (R \cap L) = P (R) \times P (L | R) = P (L) \times P (R | L)$

which means that

$P (L | R) = \frac{P (R | L) \times P (L)}{P (R)}$

And that's Bayes' theorem. It wasn't difficult to work out, and it might not look anything special, but it's doing something humans need to do all the time: it's telling us how likely something is - to what extent we should believe it - based on available evidence.

Meanwhile,in the TV studio...

... the host in the twinkling jacket is waiting for your answer as he stands beside the three doors: one open, two closed.

What you want to know are two probabilities: the probability that the car is behind door A and the probability that it is behind door C (you know that it's not behind B), given the available evidence. That phrase - given the available evidence - tells us we're dealing with conditional probabilities, so Bayes' theorem is an appropriate tool (although not necessarily a useful one). Let's see what it can do.

What's the probability the prize is behind door A given that:

you chose A and
the host opened B?

Bayes' theorem says:

P (behind A | opened B) = \frac{P (opened B | behind A) \times P (behind A)}{P (behind B)}

Let's try and give numbers to these probabilities:

$•$ If the prize was behind door A, the host could have chosen to open either B or C to reveal a dustbin. Assuming he made the choice randomly, the probability of him choosing to open B was1/2:

$P (opened B | behind A) = 1 / 2$

$•$ Without the evidence we have from which door the host chose to open, the probability that the prize was behind door A was 1/3:

$P (behind A) = 1 / 3$

So the expression for $P (behind A | opened B)$ is,

$\begin{matrix} P (behind A | opened B) & = \frac{1 / 2 \times 1 / 3}{P (behind B)} \\ = \frac{1}{6} \times \frac{1}{P (behind B)} \end{matrix}$

Now, what does Bayes have to say about the probability the prize is behind door C?

$•$ If the prize is behind C and you chose A, thehost had no choice about which door he opened - it had to be B. So

$P (opened B | behind C) = 1$

$•$ Without any evidence, the probabilitythe prize is behind C is the same as the probability it is behind A, namely $1 / 3$ :

$P (behind C) = 1 / 3$

So:

$\begin{matrix} P (behind C | opened B) & = \frac{P (opened B | behind C) \times P (behind C)}{P (behind B)} \\ = \frac{1}{3} \times \frac{1}{P (behind B)} \end{matrix}$

The prize must be behind either A or C, so

$\begin{matrix} P (behind A | opened B) + P (behind C | opened B) & = 1 \\ (\frac{1}{6} + \frac{1}{3}) \frac{1}{P (B)} & = 1 \\ P (B) & = \frac{1}{6} + \frac{1}{3} \\ P (B) & = \frac{1}{2} \end{matrix}$

Now we know P(B), we can say that

$P (behind A | opened B) = 1 / 3 and P (behind C | opened B) = 2 / 3$

It's twice as likely the prize is behind door C, compared to door A, so you should switch your choice toC.

What if the game show host had thrown open door C when you made your choice, instead of door B? You could work out the probabilitites yourself, but the result is again that you have a better chance of winning if you switch doors after one dustbin is revealed.

Without probability and Bayes' theorem, it's difficult to get a handle on what's going on here. In fact, when the problem waspublished in an American magazine, with the assertion that the best thing to do was to switch your choice, thousands of people wrote in to tell the authors they'd got it wrong. Bayes' theorem not only allows you to solve the problem correctly (if you're still not convinced, you could try it yourself, using rolls of a dice to decide where the prize is and which door is opened), but it would solve similar problems too. For example, you could use it for a similar game with four doors, where the host opens one, allows you to switch if you like, then opens another and asks again whether you'd like to switch.

What else is Bayes' theorem for?

Cheesy game shows aside, Bayes' theorem is useful in any number of other places.

Say you're playing a (fairly dull) game involving tossing a coin. You win every time the coin comes up heads. After 10 throws, only 3have been heads so you begin to wonder whether the coin is biased.

Now, youcould work out the probability of a fair coin giving you the result you have and claim that the coin is biased if this probability is below a certain level. That would give you a definite answer:"fair" or "unfair". Alternatively, you coulduse Bayes' theorem towork out two probabilities given the results: that the coin had a 50% chance of scoring a head, and that it had a 30% chance. Then you could compare the probabilities you'd worked out, which would not only tell you which hypothesis was more likely, butalso by how much. Bayes' theorem shows more clearly that we still can't be certain whether the coin is biased or not, and tells us exactly how unsure we are.

Remember in the Monty Hall problem, when we wanted to know the probability the prize was behind door A given the evidence (

P (behind A | opens B

), we had to say what the probability was without any evidence (

P (behind A)

)?Well exactly the same would apply if you wereworking out whether the coin was biased: you have to say how likely it was the coin was biased before you had any results to work fro.That's another of the strengths of a Bayesianapproach - if you don't trust the friend you're playing the coin-tossing game with, you can take this into account.
Aprobability like "the probability that the coin is biased" is not quite the same as "the probabiltity that the next throw is a head". The next throw is not decided yet, and it could be heads this time and tails next time. But the coin is either biased or it's not and however many times you check, the answer won't change. When we say "the probability that the coin is biased", we're using probability to describe how strongly we believe something to be true. If the probability is 1, I'm convinced it's biased, and if it's 0.5 I have no idea whatsoever.

In courts, where the jury are asked to decide how likely it is someone committed a crime, it's this kind of probability we're dealing with so Bayes' theorem can also be valuable. Using probability in court like this is controversial though, becauseit can be counter-intuitive and because the consequences of getting the answer wrong could be so serious.