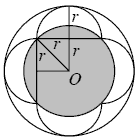
From the symmetry of the figure, the two circles must be concentric. Let their centre be O. Let the radius of the semicircles be

r

. Then the radius of the outer circle is

2 r

and, by Pythagoras' Theorem, the radius of the inner shaded circle is

\sqrt{r^{2} + r^{2}}

, that is

\sqrt{2} r

So the radii of the two circles are in the ratio $\sqrt{2} : 2$ , that is $1 : \sqrt{2}$ , and hence the ratio of their areas is $1 : 2$ .