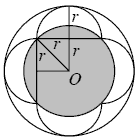
From the symmetry of the figure, the two circles must be
concentric. Let their centre be O. Let the radius of the
semicircles be r. Then the radius of the outer circle is 2r and,
by Pythagoras' Theorem, the radius of the inner shaded circle is
, that is Ö2r. So the radii of the two circles are in the ratio Ö2:2, that is
1:Ö2, and hence the ratio of their areas is 1:2.