When we think of negative numbers, they seem perfectly natural to us. That's because we've been taught to see numbers as a continuous number line, stretching out from zero in both the positive and negative directions. To us, -3 is just as real as +3 is, but this was not always the case. Negative numbers have only fairly recently become accepted as part of the system of numbers that mathematicians are allowed to use. While a great deal of very advanced maths was developed by ancient civilisations, mathematicians in most cultures had no understanding of what a negative number could mean. In this article we're going to explore some of the earliest appearances of negative numbers and how attitudes towards them have changed over the centuries.

Among the earliest people to use negative numbers in calculations were the ancient Chinese. They used counting rods to perform calculations, with red rods for positive numbers and black rods for negative numbers. The example below shows some Chinese numerals represented by rods, and the diagram on the right shows which numbers these symbols represent.

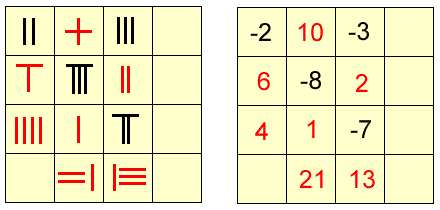
Using this system, Chinese mathematicians were able to solve simultaneous equations. Reading the numbers from top to bottom, the grid above actually represents the set of equations that we would write as:

-2x+6y+4z=0

10x-8y+z=21

-3x+2y-7z=13

Indian mathematicians also used negative numbers long before Western civilisations. An ancient manuscript from 200 BC shows that they used to use the + sign that we now associate with addition and positive numbers, to denote a negative number. Although negative numbers were used in calculations, negative answers to mathematical problems were usually considered meaningless and were discarded.

The ancient Greeks also dismissed any solutions to equations that came out negative. They called them "absurd" and "impossible" and completely ignored them. They couldn't see how a negative answer could be meaningful, because it was not possible to have a quantity that was less than nothing . This opinion was passed down to later mathematicians in Europe for more than a thousand years, so very little progress in negative number arithmetic was made for a long time.

Can you think of something in the real world where you can have a negative quantity that actually means something? Today we are quite familiar with the idea of somebody being in debt and therefore having a negative amount of money. It means that they have no money in their possession, and actually owe someone else money as well. It's not a very nice position to be in, but debt is a form of negative quantity that has been around for thousands of years. In fact calculations involving money were the only ones that were allowed to have negative answers, but most mathematicians weren't interested in that kind of problem.

So, even though everyone was quite happy to allow subtraction, and could understand the notion of debt, it took centuries before mathematicians understood or accepted that negative numbers could exist as genuine numbers in their own right. In 1759 Francis Meseres wrote that negative numbers:

"darken the very whole doctrines of the equations and to make dark of the things which are in their nature excessively obvious and simple. It would have been desirable in consequence that the negative roots were never allowed in algebra or that they were discarded" .

Even as late as 1803 the famous French mathematician Carnot was worried about the reality of negative numbers:

"to really obtain an isolated negative quantity, it would be necessary to cut off an effective quantity from zero, to remove something of nothing: impossible operation. How thus to conceive an isolated negative quantity?"

Some mathematicians in the 17th century discovered that negative numbers did have their uses. Provided they didn't worry about what negative numbers meant, and more particularly what the square roots of negative numbers meant, they found that they could solve some very tricky equations, like cubic and quartic equations. What's more, although the intermediate steps of a calculation may have involved negative numbers, the solution often came out as a real, positive number which was exactly what they wanted.

Since then mathematicians and scientists have found all sorts of uses for negative numbers. We now recognise that in many cases a negative answer can be a real, meaningful solution, but one that indicates direction . For instance, if I wanted to calculate how many steps forward Robert has taken, and the answer is -5, then it means he has taken 5 steps backwards. The first person to recognise the link between negative numbers and direction was John Wallis, a mathematician in the 17th century. He was the first to come up with the idea of a number line as a geometrical representation of the number system. Confusingly however, he also thought that negative numbers were larger than infinity!

Nowadays we use negative numbers just like any other numbers without even a second thought. Their troubled history shows how the simple mathematical principles we take for granted have taken thousands of years to develop. Physical meaning has given way to algebraic utility, but negative numbers and their derivatives have turned out to have all kinds of practical applications. Take the square root of -1 for example - it seems meaningless in itself, but many calculations in science and engineering wouldn't be possible without it.