[To do: inverse all images]Previously in this video & this
other resource we introducesd the Conway Rope Trick. You might
have noticed that two turns actually gave the same knot (and so
the same number), even if it doesn't initially look the same.But
why does it work? In this article we shall firstly spot some more
symmetries, then we will try and understand them, going on to
look at the trick in a slightly different way by doing some
different moves instead of the turn.
Often in mathematics we find it useful to talk about a general
object of a certain type, without worrying about exactly what it
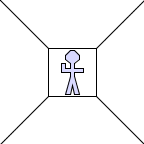
is. For this reason, we will use a picture of a man (and
occassionally a picture of a woman) to replace some messy
tangle:
or < Wtangle.png>
So it is interesting to notice that applying to turns to the knot
gives you the same knot. So:
< Something> and rot2(something)
are the same tangles. But this is true for any tangle, so we will
replace the tangle with our little man. So:
and rot2(mantangle) are actually the same tangles.
The knot is also has some more symmetry though. If you draw an
axes either vertcially or horizontally through the middle of the
knot and rotate 180 degrees, you still have the same tan\gle.
So:
< Lots of trappedmen>
Are all the same! This is quite surprising and not at all
obvious, so you might like to take two pieces of string, fix the
ends, and try to destort one until it looks like the other.
Why is this the case though? It isn't at all obvious when you
first look at the knots, they are completely different knots. So
we need to convince ourselves that it will always be true (since
otherwise someone may come up with a knot tomorrow which isn't
symmetric). To
The first thing we are allowed to do is to Twist on the right
hand side as we did before:
< m+Twist, in conway (inverse geomlab)>
The other thing we can do is twist from the bottom:
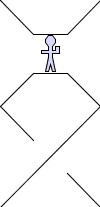
We are also allowed to add tangles horizontally:
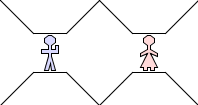
Or Vertically:
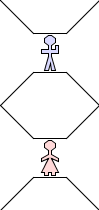
Do you notice that we can actually make any tangle that we were
able to make before? The first question you may ask is that why,
when it is rotated by two turns, we get the same diagram again
(if you don't believe this is happening, you should play with
some ropes and convince yourself this is true) ? To prove this,
we have to use induction. We can form any tangle we like by
forming a combination of the knots shown above. If you just do
twists in one direction, then it is easy to see that it is true.
Now we assume that after having made a tangle from a combination
of the elementary tangles, then it is the same if rotated about
the horizontal and vertical axes (and hence also when rotated by
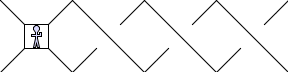
two turns). So we assume that:
is the same as
which is the same as 
.
But now you can add another elementary twist operation, either
horizontally or vertically, and the object still has the same
symmetry. For example, if we add three twists to the right to
create the new shape:
and then rotate it around two turns
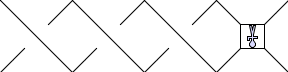
We would like this to be the same as the first shape. To do this,
we can rotate the whole thing around three times, keeping the
ends fixed to give:
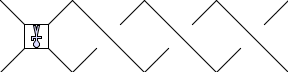
But then we know that reflection in the horizontal axes leaves
the man unchanged, so the two are the same!
We could similarly check all the other properties, and so we now
know that if a tangle formed by a combination of n elementary
tangles is left unchanged by rotation, or flipping in the
horizontal or vertical axes, then one made from n+1 elementary
tangles also does. But we can now use the power of mathematical
induction, since if it is true for one n, it is true for all n
above this. But it is true when n=1, so it is true for all values
of n. So any tangle is left unchanged by flipping in the
horizontal or vertical axes, or rotations by two turns (if you
wish to learn more about mathemtical induction, you may wish to
read
this article ).
********************************************************************************
[INSERT DEFINITIONS]
Using this we can notice that t'_a=1/t_a, and
t_a+'t'_b=1/(t_b+1/t_a) - You might like to have a go at drawing
diagrams to show this before you continue reading.
But we constructed the initial tangle by alternating between
twists of the t_a type and the t'_a type, and so we can write a
triangle as a continued fraction of the form:
from which we get our number for the tangle:
A useful formula from Lagrange for this is:
Which can be applied carefully to any continued fraction and
applied physically to the tnagle to get a new continued fraction
for the same number, but with all of the terms except the first
positive. The continued fraction in this form is unique though.
So now, if we have two tangles, with the same number, we can get
them both into the form with the same continued fraction
representation, and so we can make them appear in the same. So a
tangle is uniquely identified by its continued fraction
[Do it topologically? - pg 317]
References :
Jay R. Goldman and Louis H. Kaffman. Rational Tangles.
Advances in Applied
Mathematics , 18(AM960511):300-332,1997