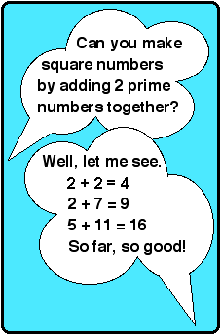Using non-standard problems to
challenge pre-conceptions: can they extend knowledge?
Jenni Back, Jennifer Piggott and
Liz Pumfrey.
Primary Mathematics Project,
Faculty of Education, University of Cambridge.
This paper will explore the value of using
problems as a way of challenging children's mathematical
pre-conceptions and explore their potential for extending their
knowledge and understanding. It will do this by considering some
non-standard problems taken from the NRICH website
(www.nrich.maths.org) and by considering children's responses to
them. The value of such problems will be examined in the light of
what children have said, or implied, about their thinking by
examining their solutions.
On the NRICH website we offer a variety of resources for children
and teachers to enrich children's mathematical experiences. These
include open ended investigations, problems, games, activities
and articles, some of which involve an interactive component. New
problems are posted on the website nine times a year and we post
solutions to the problems that children send in. This opportunity
for students to present their work to an interested audience
gives us feedback on what some children make of our problems,
their strategies for solving them as well as some indications of
the preconceptions, knowledge and understanding they bring to
them.
For the purposes of this paper we will take a problem that we
have presented on the website and examine the rationale for using
it as well as what some of the solutions that we have received
tell us about children's responses to the problem. The problem is
on number but many other topics are covered on the site.
The following question has Content Level 2 and Challenge Level 1.
This means it requires knowledge of curriculum content usually
met by the age of 12 years and will be challenging for the
"average" pupil. The focus is on non-standard problems that
encourage children to think mathematically and to bring aspects
of their mathematical knowledge and understanding to bear in an
unfamiliar context. This question considers the relationship
between prime and square numbers in a novel context:
The Problem
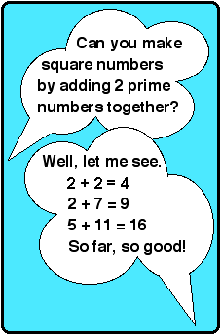
- Try with the squares of the numbers between 4 and 20.
- Did you find any square numbers which cannot be made by
adding two prime numbers together?
The Rationale
The initial focus in this question seems to be the question in
the bubble in the blue rectangle. Taken from this starting
point, the problem is challenging for children as it asks them
to explore a connection that they have probably not thought of:
What is the relationship between prime numbers and square
numbers? Is there any link?
This making of connections is widely considered to be an
essential component of effective learning and teaching of
mathematics. (Askew, Brown et al. 1997) The question (to the
side) offers the potential to make the problem accessible to a
wider audience by including some calculation practice as a
preliminary task and offering a way into the problem that
provides information for the main activity. This creates a much
stronger motivation for the children than simply finding the
square and prime numbers.
Anne Watson (2002) suggests that one of the most efficient ways
of getting learners to extend their "example spaces" is by
imposing constraints. These example spaces are the set of
examples that individuals can call to mind when working on
known concepts. In relation to this problem we would suggest
that simply getting pupils to find square numbers or prime
numbers does not help to develop their understanding of the
nature of either as much as this juxtaposition to the two. The
"can you make" question offers a restriction that challenges
thinking and so helps them to extend their example spaces.
The question in the bubble combines the separate ideas about
square numbers and prime numbers into a single context,
inviting students to make mathematical connections.
The Solution
We received a number of good solutions and posted the following
answer on the website:
This question has been very well answered - thank you to
everyone who sent us solutions.
D, J and M from Year 5 and B, H and He from Year 4 at St.
Nicolas CE Junior School, Newbury explain how they tackled it:
"We listed the prime numbers up to 100 and then we listed the
squares of the numbers between 4 and 20. Then we started
working out the answers by adding two prime numbers together to
make the squares until we reached 400. We found out that two
squares were impossible to make. When we had an odd square
number, we had to have a number that adds on to 2 to make the
square number and sometimes this number wouldn't be prime. For
example, to make 121 with two primes, one of the primes has to
be 2, and 119 is not prime.
Our results were:
|
|
Once the calculation is done, the thinking starts. How can we
make the numbers by adding two prime numbers together? Are the
solutions presented here the only possible option in every
case? With the odd numbers, the solution has to involve 2 and
another odd number. Why?
It may be obvious to us that two is the only even prime and
that two odds added together make an even number every time but
children may not be fully aware of this information or have it
as part of their repertoire of problem solving skills.
This solution shows evidence of a child engaging with some
sophisticated reasoning about the relative sizes of numbers,
the digits involved in their construction, and the ways in
which they can be ordered. We would like to suggest that this
is the product of a non-standard problem that offers a real
challenge and involves mathematical thinking to reach a
solution. Taking John Mason and Anne Watson's (1998)
descriptions of mental activities that typify mathematical
thinking, we would suggest that the solution shows evidence of
sorting, organising, changing and comparing systematically as
well as routine calculating procedures. Solutions do sometimes
offer insights into some of the pre-conceptions that children
might have, although in this case the solution reveals very
limited information along these lines. Our knowledge of
children's experiences of mathematics in school would suggest
that it is likely that the children often expect maths to be a
very compartmentalised subject and involve routine practice of
procedures (Boaler 1997) rather than novel problems. As such
this question would challenge them: they are being expected to
think about and around a mathematical situation rather than
practise a familiar technique. In doing so, they have the
opportunity to extend their knowledge of the connections
between different aspects of mathematical practice. The problem
is an elementary one but links square numbers with ideas about
prime numbers as well as a consideration of addition and so
challenges pre-conceptions that different mathematical ideas
can be separated into different boxes.
From this example we do not have hard evidence that the
children's knowledge or understanding have improved. However we
can suggest that the challenge involved is likely to extend the
boundaries of their knowledge and understanding as well as
connections between different mathematical ideas. This is
supported by our observations of children who work on our
problems and who frequently make comments about how they have
gained knowledge and insight mathematically from their work.
In posting solutions from children we seek to demonstrate the
communicative aspects of mathematics and emphasise the
distinction between solutions and answers: a solution
communicates the mathematics but an answer is the end. The
communication of mathematics is, we believe, an essential part
of its purpose: it is not an isolated activity undertaken by
people in corners or dark alleys or even ivory towers.
Non-standard tasks help to develop this repertoire by
emphasising the need for "thinking around the problem" and
sharing outcomes. In the presentation of the chosen solution we
have deliberately picked one which shows clear reasoning and a
justification for the answer. By having to justify their
findings to an audience the students are encouraged to think
about the key mathematical ideas that underpin their solution
and make sure they are clearly articulated to others. In this
way the child is applying knowledge in new contexts and hence
extending their repertoire of experiences on which to base
future work, they are improving understanding by making
connections between the properties of primes (only one even
prime) and the properties of square numbers. A range of
mathematical concepts are being drawn together to encourage
students to make connections and hence improve their
understanding.
We would suggest that non-standard problems are able to
challenge pupils' preconceptions by exposing them to unfamiliar
contexts in which routine procedures will not offer them easy
answers. Instead they are encouraged by the contexts of the
problems to think about what they know mathematically and
consider it in the light of this new problem. In doing so they
develop their ability to make mathematical sense of the problem
and so increase their knowledge and understanding of the
related mathematical ideas, techniques and strategies.
References
Askew, M., M. Brown, et al. (1997). Effective Teachers of
Numeracy. London, School of Education, King's College London:
122.
Boaler, J. (1997). Experiencing School Mathematics: Teaching
styles, sex and setting . Milton Keynes, Open University
Press.
Watson, A. (2002). Exploring example spaces: what are they like
and how do we move around them?
Watson, A. and J. Mason (1998). Questions and Prompts for Mathematical
Thinking . Derby, Association of Teachers of
Mathematics.
This paper was first
published in Conference Proceedings, International Symposium
Elementary Maths Teaching, Charles University, Prague in
2003.