Let T be the centre of
the semicircle with diameter QR and let OT produced meet the circumference
of the larger semicircle at U .
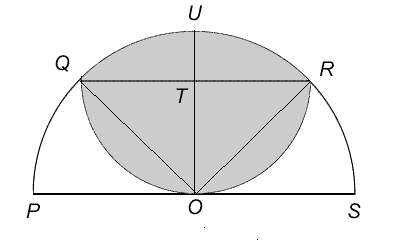
By symmetry, we note that OT is perpendicular to QR . As TR = TO = TQ (radii of the same
semicircle), triangles ORT and OQT are both isosceles, right-angled
triangles. So QOR is a
right angle.
By Pythagoras' Theorem: QR ² = OQ ² + OR ² = 2² + 2² =
8.
So QR = Ö8 = 2Ö2 and the radius of semicircle QORisÖ2.
The area of the shaded region is equal to the area of
semicircle QOR plus
the area of the quadrant bounded by OQ , OR and arc QUR less the triangle OQR .
So the required area is
+
- (
) = p+ p- 2 = 2p - 2.
