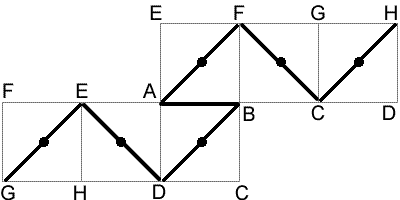
The image above shows a possible path. Each edge joining a corner to a face centre has length

\frac{1}{\sqrt{2}}

(by Pythagoras' Theorem), while each edge which joins two adjacent corners has length 1. So the length of the path above is

1 + 6 \sqrt{2}

. This is the length of the shortest path to pass through all the vertices.

To prove this, note the length of the shortest path must be at least $\frac{13}{\sqrt{2}}$ . Such a path would move alternately between corners and faces, but as there are 8 corners and only 6 faces, so this is impossible. So at least one of the edges must join to corners, and so the shortest length is $1 + 6 \sqrt{2}$ .