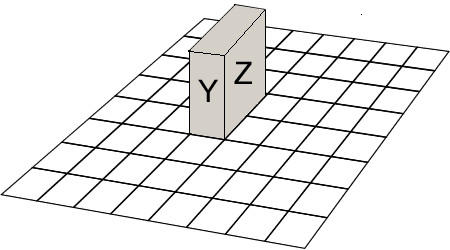
A 1×2×3 block is placed on an 8×8 board, as shown with the
1×2 face X at the bottom.
It is rolled over an edge without slipping onto a 1×3 face Y,
then onto the 2×3 face Z,then onto X, Y, Z again in that order.
How many different squares on the board has the
block occupied altogether, including the starting and ending positions?