Simon from Elizabeth College, Guernsey and Andrei from Tudor Vianu National College, Romania have both solved this problem and both solutions are used below.
 |
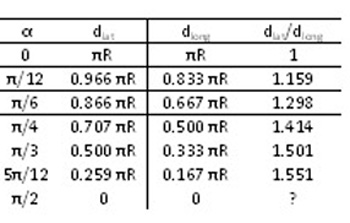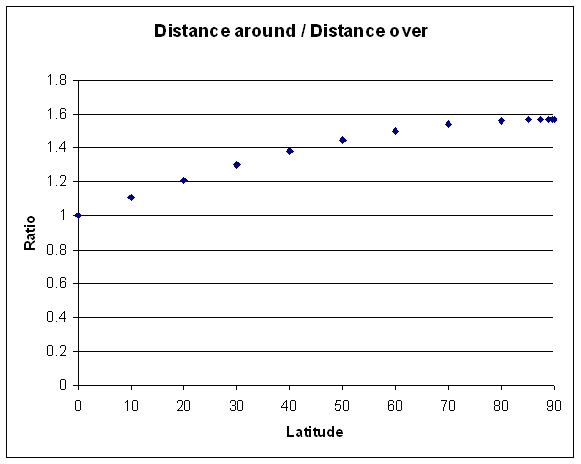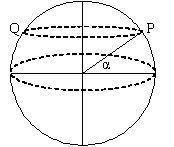
To solve this problem we shall consider that the point
is situated at latitude $\alpha$. To travel around the
line of latitude, the distance from P to Q would be
half the circumference of the circle at latitude
$\alpha$. This circle has a radius $R \cos \alpha$,
where $R$ is the radius of Earth.
So, the distance traveled from P to Q on the line of
latitude is $d_{lat} = \pi R \cos \alpha$.
|
| Traveling over the line of longitude, the circle on which we have to calculate the distance is a great circle of the sphere, and the angle of displacement is 2(p/2 - a) radians. The distance is therefore 4pR(90-L)/360 where L is the angle of latitude in degrees or equivalently dlong = 2R (p/2 - a). It is clear that the path on a great circle is always shorter. |  |
 |
A graph of the ratio of these distances
shows that this ratio seems to tend to
p/2 as the line of latitude approaches
the pole, that is the ratio
as q® 0 we can take q = p/2 - a and we see that this limit is p/2. |
|