Two polygons fit together so that the exterior (orange) angle at each end of their shared side is 81^°.
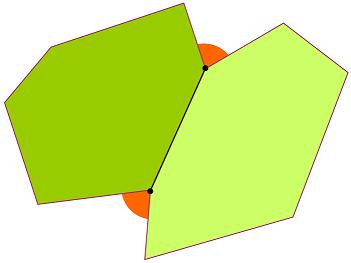
If both shapes now have to be regular polygons, but do not need to be the same, and each polygon can have any number of sides, could the orange angle still be 81^°, and if that is possible how many sides would each polygon have?

Find solutions for when the orange angle is 27^° and when it is 54^°.

Can you make a conjecture about the connection between the size of the orange angle and the number of sides on each polygon.
If you can, are you able to justify your conjecture?