Andrei from Romania sent in a good solution to this problem.

(1)(a) We have to show that $qq^{-1} = 1$: $$q^{-1} = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i}) = {1\over 2}(1 - {\bf i}^2) = 1$$ (b)Take $x = ti$ to be any point on the x-axis. Then $qx = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t{\bf i} = {-1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t = xq.$

We have shown that $qx = xq$ and so $qxq^{-1} = x$.

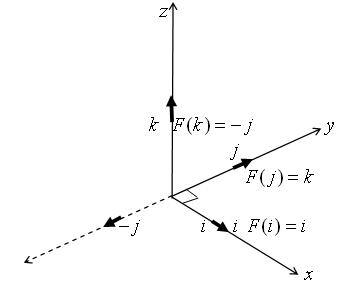Let $F(v) = qvq^{-1}$ be a mapping of points $v$ in $R^3$ to images in $R^3$ where the 4-dimensional quaternion $q$ acts as an operator. We have proved that this mapping fixes every point on the x axis.

(c)What effect does this mapping have on other points in $R^3$? $$F({\bf j})= qjq^{-1} = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})({\bf j}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i})$$ $$ = {1\over 2}(1+{\bf i})({\bf j})((1 - {\bf i})$$ $$ = {1\over 2}({\bf j} + {\bf k})(1 - {\bf i})$$ $$ = {1\over 2}({\bf j} + {\bf k} + {\bf k} - {\bf j})$$ $$= {\bf k}}.$$ Similarly $F{\bf k} = -{\bf j}$. Parts (b) and (c) together show that the mapping $F(v) = qvq^{-1}$, where $q = \cos (\pi /4) + \sin (\pi /4) {\bf i}$, gives a rotation of $\pi /2$ about the x axis.

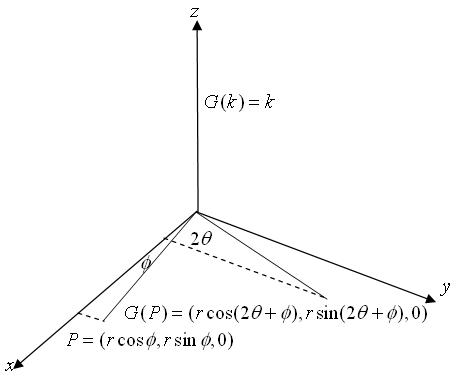(2) In this section we consider the mapping

G (v) = {qvq}^{- 1}

R^{3}

R^{3}

where the quaternion

q = \cos θ + \sin θ k

is an operator.

(a)

(\cos θ + \sin θ k) (\cos θ - \sin θ k) = \cos^{2} θ + \sin^{2} θ = 1

so these two quaternions are multiplicative inverses.

(b) We have $qk = - \sin θ + \cos θ k = kq$ and hence ${qkq}^{- 1} = k$ . So the mapping $G (v) = {qvq}^{- 1}$ fixes the z-axis.

(c) What effect does the mapping $G$ have on vectors in $R^{3}$ ? We consider the vector $v = r (\cos ϕ i + \sin ϕ j)$ .

$\begin{matrix} {qvq}^{- 1} & = & (\cos θ + \sin θ k) r (\cos ϕ i + \sin ϕ j) (\cos θ - \sin θ k) \\ = & r ((\cos θ \cos ϕ - \sin θ \sin ϕ) i + (\cos θ \sin ϕ + \sin θ \cos ϕ) j) \cos θ i - \sin θ k) \\ = & r (\cos (θ + ϕ) i + \sin (θ + ϕ) j) (\cos θ i - \sin θ k) \\ = & r ((\cos (θ + ϕ) \cos θ - \sin (θ + ϕ) \sin ϕ) i + (\cos (θ + ϕ) \sin θ + \sin (θ + ϕ) \cos phi) j) \\ = & r (\cos (2 θ + ϕ) i + \sin (2 θ + ϕ) j) \end{matrix} .$

cylinder We have shown ${qkq}^{- 1} = k$ so $G (v + tk) = q (v + tk) q^{- 1} = {qvq}^{- 1} + {qtkq}^{- 1} = {qvq}^{- 1} + tk$ for all $t$ .
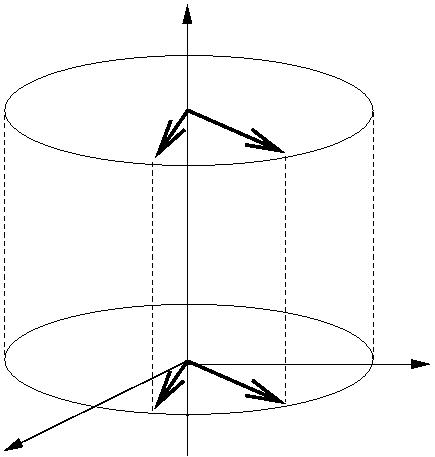
We can see that the vector $v$ in the $xy$ plane is rotated about the $z$ axis by an angle $2 θ$ and all points on the vertical line through it are also rotated about the $z$ -axis by an angle $2 θ$ .
So by the mapping $G (v) = {qvq}^{- 1}$ all points in $R^{3}$ are rotated by $2 θ$ about the $z$ -axis.
Note that, for any rotation of $R^{3}$ , we can make a transformation of the coordinate system so that the axis of the rotation is made to coincide with the $z$ -axis, then perform the rotation by the given angle about the $z$ -axis, and finally transform back to the original coordinate system.