Here are two solutions, one from Simon
from Elizabeth College, Guernsey and one from Andrei from Tudor
Vianu National College, Bucharest, Romania. First Simon's
solution.
The functions are:
Firstly I looked at Archimedes' choice, the logarithmic function.
|
A(n) = log(100n) = log100 + logn. |
|
I knew that when n gets large log100 would become irrelevant.
This meant that only logn would be important, and logn < n
when n > 1. So A(n) will be less than n for large n. We
find n = log(100)+ logn for n = 6.472775 approximately and so
A(n) < n for all values of n > 6.5.
The next task was establish whether B(n) or C(n) was greater for
large numbers. I was certain of one thing: B(n) = C(n) = 100100
for n=100.
Firstly I knew that 100n would have 2n+1 digits. I then
established, where x is the number of digits in n, that
n100 would have between 100(x-1)+1 and 100x digits. So
C(n) = 100n is the larger function for n > 100.
Therefore, so far, C(n) is the largest function for large values
of n.
The next task was to compare it to D(n) or factorial n.
Using Stirling's formula:
|
D(n) = n! = |
Ö
|
2pn
|
|
æ
ç
è
|
n
e
|
ö
÷
ø
|
n
|
. |
|
As n is a large positive number,
will be greater
than 1. Therefore when n/e is greater than 100, D(n) > C(n). The 'change over point' occurs for n just less than n = 100e, that
is n » 270.
Andrei considered the natural
logarithms of the functions and plotted their graphs. For the
factorial n function Andrei used Stirling's Approximation which
is valid for large n.
I approximated the function for factorial n further by
ignoring the term
.
I know that log(n) < n
for the whole domain of definition of the logarithmic function, and
I see that A is the smallest. I have to compare the other
functions. As log(100) » 4.60, so:
In the limit for large n,
and so B < C.For
large n we can neglect 1 in respect to log(n) in the
approximate formula for log(D) and, as 4.6 < log(n) we
have D > C > B > A.
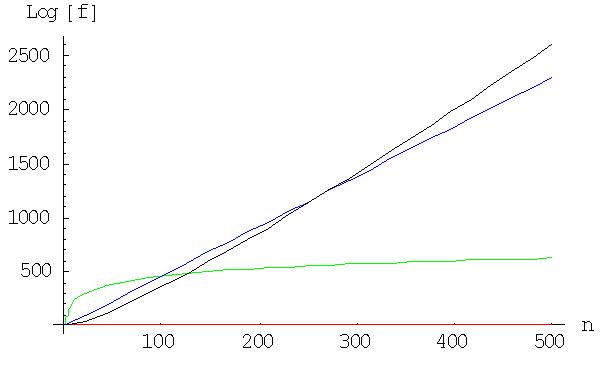
Here in the diagram, A(x) is represented in red, B(x) in green, C(x)
in blue and D(x) in black.
It can be observed that for large n (here n > 300)
the order of the magnitude of the functions is D > C > B > A.