We received correct solutions from Ash and
Lucy, two students at Tiffin Girls' School. Well done to you
both.
Ash sent us this correct solution:
The gradient of the first line must be the negative reciprocal
of the gradient of the other line:
if you multiply the two gradients you always get -1.
For example:
Take a random gradient, say
The negative reciprocal gradient will be
Make up two equations with these gradients, say
and
Draw them on a grid
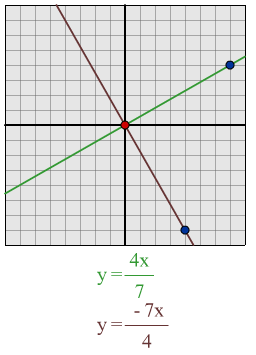
You get perpendicular lines.
Lucy recorded how she worked through this
problem:
y = x
is perpendicular to y =
-x
y = x is perpendicular to
y = -x + 2
(the y-intercept doesn't affect the gradient of the line)
y = 2x is perpendicular
to y = -x/2
y = -3x is perpendicular
to y = x/3
(to make a line perpendicular you need to invert the gradient,
or take the reciprocal, and change the sign)
y = -2x is perpendicular
to y = x/2
I can see a pattern here: when the two gradients of perpendicular
lines are multiplied together they give -1, and the y-intercept
does not affect if the line is perpendicular or not.
I will now try to work out what the perpendicular line of some
other lines will be using this formula:
y = 7x - 3
Using my formula I predict that a line which is perpendicular to
this line will be y = -x/7 -
3
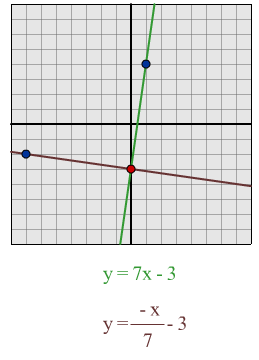
When I tested the lines out, I found that the formula had
worked.
y = x/3 + 4
Using my formula I predict that a line which is perpendicular to
this line will be y = -3x +
4
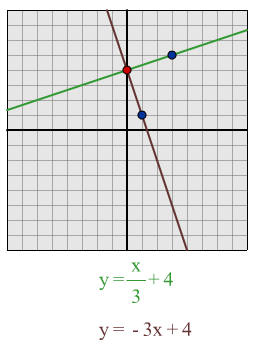
Having drawn out the lines I found that the formula worked and
the lines were perpendicular.
y = -7x/3 + 2
I predict that a line which is perpendicular to this line will be
y = 3x/7
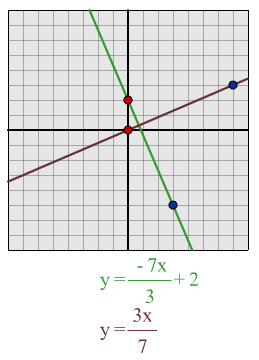
From drawing out these lines I can see that they are
perpendicular.



