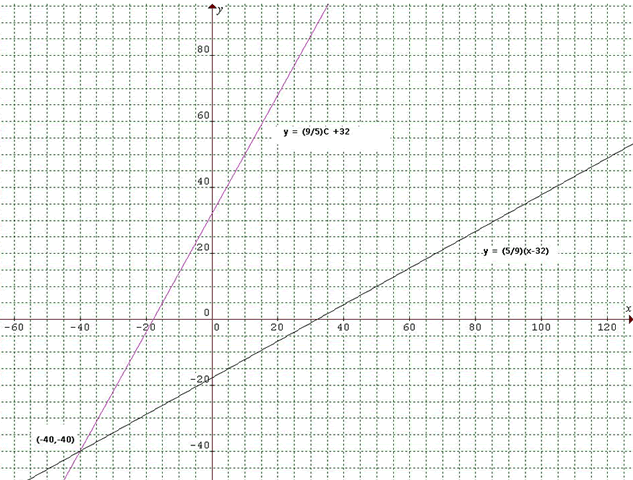The answer to this problem is yes, there
IS a temperature where Celsius and Fahrenheit are equal, and it
is -40 degrees.
All the solutions to this problem took
one of three forms: trial-and-improvement, graphical or
algebraic:
This is how Samuel from Long Buckby
Junior School reasoned:
There is a temperature at which Celsius and Farenheit are the
same.
It is -40 degrees, because 9/5 of -40 is -72 and -72 + 32 = -40.
I decided to look at negative numbers because starting with a
positive number and multiplying it by 9/5 is going to increase it
and so is adding 32 so you're always going to end up with a
number greater than the number you started with.
However, if you you start with a negative number, multiplying it
by 9/5 decreases it, and adding 32 increases it, so I realised
that with the correct number, Celsius and Fahrenheit might be the
same.
I decided to go down in tens:
9/5 of -10 = -18
and -18 + 32 = 14,
so that doesn't work;
9/5 of -20 = -36
and -36 + 32 = -4,
so that doesn't work;
9/5 of -30 = -54
and -54 + 32 = -22,
so that doesn't work.
But 9/5 of -40 = -72
and -72 + 32 = -40 so it works.
The reason it works is because multiplying by 9/5 is equivalent
to adding 4/5 of it, and for -40 adding 32 is equivalent to
subtracting 4/5 of it (because 32 is 4/5 of 40).
Because of this, Farenheit and Celsius are equivalent ONLY at -40
degrees.
The Four Mathemateers from Brocks Hill
Primary School also used a trial and error approach, as displayed
here:
First we started going down in tens of Celsius from 0, and we
found out a pattern:
the difference between F and C was getting closer by eights every
time.
When we got to -30C the difference was only 8. So -30C is equal
to -22F.
Then we tried -40C and found out that -40C was the same as -40F.
So the answer is -40.
Yesuhei used a similar
strategy:
First I tried different solutions for Celsius like -50 and that
gave me -58 Fahrenheit .
Then I tried -45C because whenever you go down (negative
increasing) the F and C's distance increases. That gave me -48
Fahrenheit which was very close, so I tried -40 Celsius and
that gave me -40 Fahrenheit.
Others who found the correct answer by
this method are Emma and Chloe from The Mount School and Michael
from Bilton School.
Beatrice fron Raffles Girls' School and
Michael used a graphical approach.
Michael's answer is shown here:
I plotted the lines of the simultaneous equations against each
other and found where they crossed.
In the graphs y = F and x = C.
The quickest way to solve this problem is
with an algebraic approach, and both of the people who used
graphs used this approach as well. The other people that obtained
the correct answer by this method include Sugam and Fiona from
The Mount School, Chris from CCSN, Samantha from The Steele
School, Gemma, Griselda and Charlie from Colyton Grammar School,
Jasvir, Matt and Christian from Kingshill, Ed from Tunbridge
Wells Grammar School for Boys, Stephen Joe from Singapore
International School, Kieran from Alcester Grammar School and
Pradeesha:
Here is Sugam's working:
Let x be the temperature where Fahranheit and Celsius are
equal.
5x = 9x + 160 -4x = 160 x = -40
Therefore -40 Celsius = -40 Farenheit
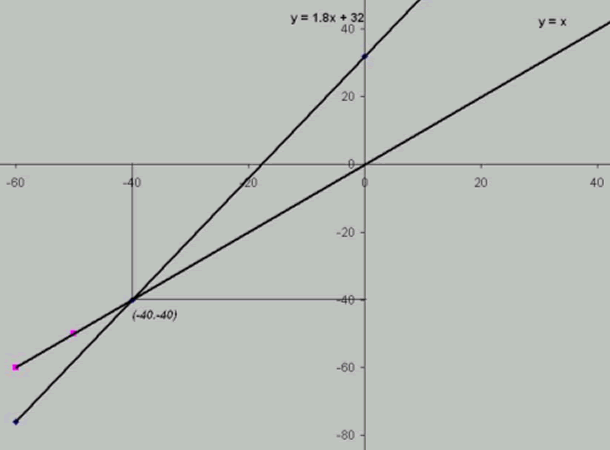
And here is Michael's solution:
To solve it algebraically I can create two simultaneous
equations:
F = C
F = 1.8C + 32
Therefore
C = 1.8C + 32
C = 32 / 0.8 = -40
And here is Kieran's solution:
Using the equation,
,
we can remove the fraction by multiplying both sides by five. Doing so produces
, and thus,
using the sought after equation of
,
we may further deduce that,
since
are one and the same,
subtracting the two equal amounts from either side leaves
or
or
Consequently, -40 Celcius is the same as -40 Fahrenheit.
Oliver remembered to check that his
solution worked:
We can substitute -40 as C in F = 9/5C + 32 to check our answer
As -40 = -72 + 32, our answer is correct
Beatrice combined an algebraic and
graphical approach:
We know that F = (9/5)C + 32 [equation 1]
This is a linear equation, because it follow the structure
y = mx + c
Now let us make C the subject:
F = (9/5)C + 32
F - 32 = (9/5)C
C = (5/9)(F - 32) [equation 2]
Now plot equations 1 and 2 on Graphmatica.
They will intersect at the point (-40,-40).
So we know that -40F = -40C.
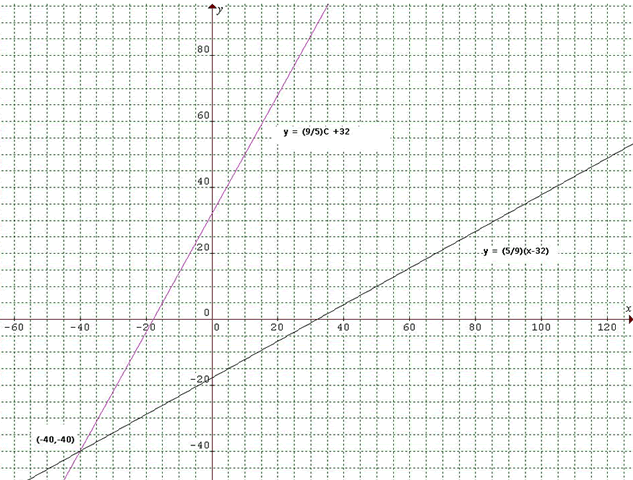
Well done to all of you who solved this
problem correctly.