The sound of bells

If you wear a different coloured T-shirt every day someone may say that you are "ringing the changes". This expression simply means that you plan for variety rather than keeping things the same. It comes from the the custom of ringing church bells.

In East Anglia, as you look across the fens, villages appear almost like little islands (indeed some of them were islands before the fens were drained) and these villages are dominated by big churches with tall towers. In the past people regulated their lives and passed messages by ringing church bells, which could be heard for miles around, telling the time of day, and giving news of births, marriages and deaths in a parish. The following quotation comes from the ringer's rules from Southhill in Bedfordshire "When mirth and pleasure is on the wing we ring; at the departure of a soul we toll".

Bell ringing is good exercise for the body and mind, the bells are heavy and the bellringers have to remember the changes. Bell ringing often appeals to mathematicians because there is a lot of mathematics to be found in these complicated sequences of changes. Before reading on you might like to try this problem on bellringing.

The mathematics of the changes

The reader is invited to investigate permutations in the ringing of church bells, that is the different orders in which the bells can be rung on a ring of bells. Each bell is mounted on a wheel and controlled by a bellringer pulling on a rope. A bell rings once per revolution. Roughly speaking it rotates 360 degrees from top-dead-centre back to top-dead-centre and strikes (once) when it is about 70% of the way round. The bell rings alternately clockwise and anti-clockwise (roughly 360 degrees each way) and two revolutions constitute a so-called whole pull. Rather confusingly a whole pull (singular) consists of two pulls (plural) on the rope.

The bellringer can speed up or slow down his or her bell to alter its turn in the order by one place, but not by more than one. Each bell is rung just once in a sequence (a row), then all the bells are rung again, but in a different order (a permutation of the previous order), then all again in a different order and so on. We say the bells are rung in rounds when the bells are rung in order with the notes descending in pitch from the lightest bell, the treble, to the heaviest, the tenor.

So for example, with just three bells there are six possible orders in which they can ring. Mathematically speaking there is a group of six bell ringing rows.

Starting with the row 123 the next could be 213 (interchanging the order of the first two ) or 132 (interchanging the order of the second two), but it could not be anything else.

When the order in which the first two bells are rung is interchanged we call the change p, and when the order of the second pair are interchanged we call the change q.

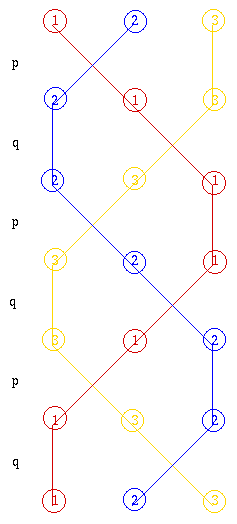
One way of ringing every posible row once beginning and ending with rounds is to ring the changes p then q then p then q then p and finally q again as illustrated by this braid diagram. Each line shows the order in which the bells are rung and the bellringers remember their 'parts' by remembering the shape and pattern of their strand in the braid.

A circuit diagram provides another way of illustrating these changes. Here we see the change p illustrated by a black line, and q by a blue line. Each node represents one of the six permutations. By traversing the circuit either clockwise or anticlockwise, we see two ways to ring a block denoted by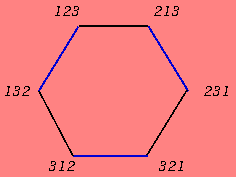

{(pq)}^{3}

and

{(qp)}^{3}

With four bells there are of course many more possibilities; there are twenty four different permutations or orders in which the bells can be rung and there are four bell ringing changes.

Braid diagram 2

Plain Hunt Minumus.

The first pair can be transposed and the second pair stay the same, we call this p, the second pair can be transposed and the first pair stay the same, we call this q, the middle pair can be transposed and we call this r, and finally both pairs can be transposed and we call this s. 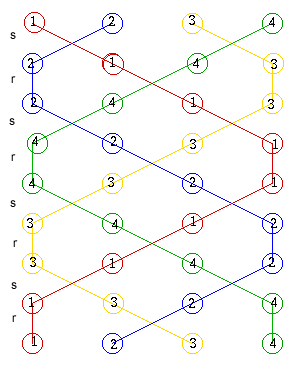The bellringers' notation records the bells that don't move so what we record as p or X|| is written 34, what we record as q or ||X is written as 12, what we record as r or |X| is written as 14 and what we record as s or XX has the special name 'cross'.

Repeating $s$ and $r$ alternately gives the sequence of changes shown in braid diagram 2 which is denoted by ${(sr)}^{4}$ representing Plain Hunt Minimus.

Braid diagram 2 does not give all 24 permutations although it does start and finish with the same row and bellringers describe this as a round block. Braid diagram 3 gives an example where all 24 rows occur once and only once and the sequence starts and ends with the same row.

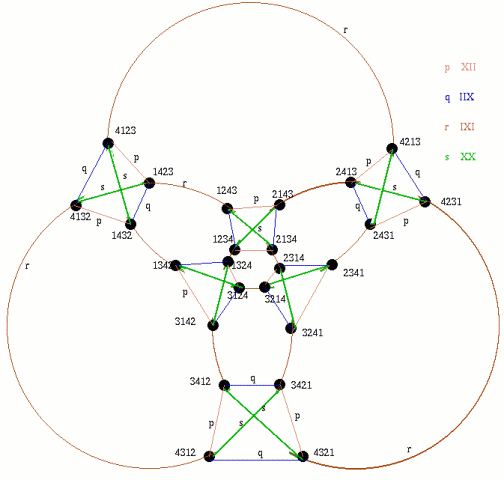
Now look at the network diagram below which shows all 24 possible permutations in the order of the four bells. This network represents all the sequences of the changes p, q, r and s for four bells in much the same way as the simple hexagonal network for three bells. Any two adjacent vertices in the network represent permutations for which there is a bell ringing change between one and the other. The four changes p, q, r and s are shown in four different colours.

Find the vertex labelled 1234. Now follow the green edge which represents the change s from 1234 to 2143. This is the first change shown in braid diagram 2 which shows the sequence $s r s r s r s r$ or ${(sr)}^{4}$ which starts and ends with 1234. This is shown in the network below by the large circular loop on the bottom right hand side. As we noted before, although this loop starts and ends at the same vertex it does not visit every vertex in the network. However, by traversing the entire network, visiting each vertex once and only once and returning to the stating point, we get an extent on four bells in which each row is rung once and only once.

Circuit diagram showing the 24 permutations of 4 bells

Bellringers are interested in different ways of ringing all possible changes without repeats which is known as an extent and braid diagram 3 shows an example of an extent on four bells.

If you start at 1234 in the network diagram above can you trace a path around the network corresponding to braid diagram 3 visiting each vertex in the network once and only once? Start at the vertex representing 1234 then follow the green path for the permutation s to the vertex for 2143, then follow the red path for the permutation r to the vertex for 2413 and so on... and finally return to the starting point along the yellow path for the permutation p from the vertex 2134 to the vertex 1234. This is denoted by ${{(sr)^{3} sp}}^{3}$ .

Can you find other Hamiltonian circuits around the network visiting every vertex once and only once, and can you draw their corresponding braid diagrams? For example, to ring what bellringers call Plain Bob, you follow the path ${(sr)}^{3} s$ and then instead of switching by $p$ from 1324 to 3124 you switch by $q$ from 1324 to 1342 and use $q$ again rather than $p$ later in the sequence giving ${(sr)^{3} sq}^{3}$ .

Each bellringer remembers his or her pattern in the braid and, in particular, the 'dodges', for example where bell number 1 permutes with 3 and then with 3 again at the first occurrence of the permutation $p$ in braid diagram 3.

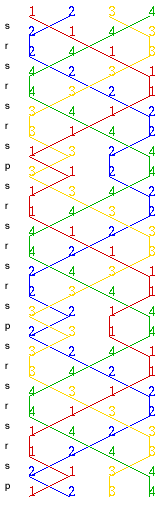
Braid diagram 3 represents

an extent on four bells.

In addition to studying the mathematics of bellringing, there is an interest in investigations into the mechanics of church bell ringing as described in this news item from the Cambridge University website of 17th January 2005:

"As part of a fourth-year student project on the mechanics of church bell ringing, a "bell tower" has been built in the Mechanics Laboratory. The bell has been instrumented to provide data on the movements of bell and clapper, to compare with a theoretical model. In this picture, the bell is being rung by Dr Frank King of the Computer Laboratory, who is the official University Bellringer. He is being watched by Professor David Newland, past head of the Engineering Department and a keen bellringer. "

A computer program can be written to play this music and readers are invited to send in their programs. You might be able to borrow some hand bells, or you could try it out on any musical instrument, or you could even tune glass bottles, with different amounts of water in them, and 'ring' the bottle-bells by striking them with a teaspoon.

The next article will explain the group theory which underlies these ideas and which is represented by the network diagram.

Further information can be found in Frank King's book Ringing Elementary Minor Methods on Handbells and on the Central Council of Church Bellringers website and the Wikepedia website and many more.