Method of taking one item from the infinite set.

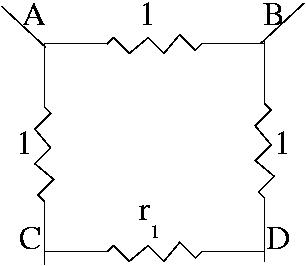
Denote the resistance of the infinite network by

R

. By removing just three resistances from the infinite circuit the resistance of the remaining infinite circuit is unchanged. The resistance between A and B is the same as the resistance between C and D cutting out the three resistances above. Hence

r_{1} = R

which gives

\frac{1}{R} = \frac{1}{1} + \frac{1}{2 + R}

and so

R = \frac{2 + R}{3 + R}

giving the quadratic equation

R^{2} + 2 R - 2 = 0

. Solving this equation, as

R \geq 0

the solution is

R = \sqrt{3} - 1

Method using a sequence and continued fractions.

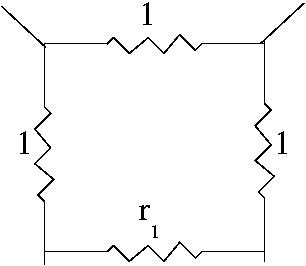In this diagram

r_{1}

replaces the total resistance of the remaining network.

Taking $R_{1}$ as the total of these 4 resistances:

$\frac{1}{R_{1}} = \frac{1}{1} + \frac{1}{2 + r_{1}} .$

So

$R_{1} = \frac{1}{1 + \frac{1}{2 + r_{1}}}$

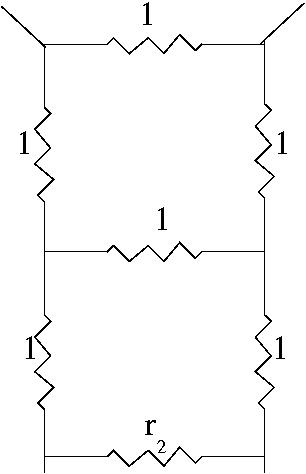
Now replacing

r_{1}

by 4 resistors where

r_{2}

replaces the total resistance of the remaining network as shown in the diagram we have

\frac{1}{r_{1}} = 1 + \frac{1}{2 + r_{2}}

r_{1}

is replaced by

\frac{1}{1 + \frac{1}{2 + r_{2}}} .

Taking

R_{2}

as the total of these 7 resistances:

\frac{1}{R_{2}} = 1 + \frac{1}{2 + \frac{1}{1 + \frac{1}{2 + r_{2}}}}

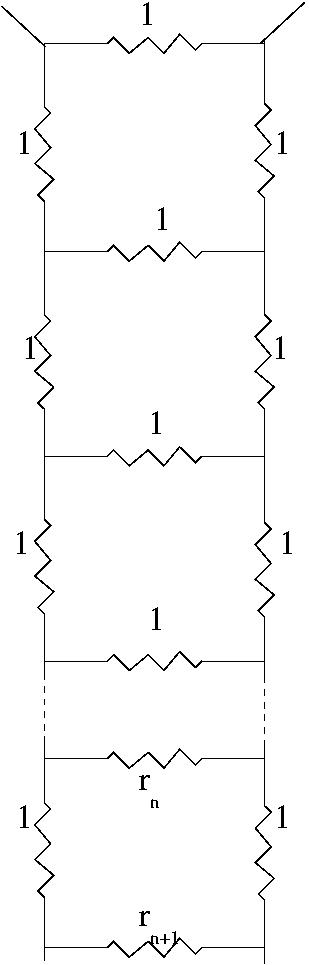Each time we add another 3 resistances to the network we replace

r_{n}

by a resistance of 1 ohm in parallel with 3 more resistances of 1,

r_{n + 1}

and 1 ohm in series such that

\frac{1}{r_{n}} = 1 + \frac{1}{2 + r_{n + 1}}

As the process continues indefinitely this gives the total resistance

R

in terms of the continued fraction

R = \frac{1}{1 + \frac{1}{2 + \frac{1}{1 + \frac{1}{2 + \frac{1}{1 + . . .}}}}} .

The periodic nature of this continued fraction enables us to calculate

R

R = \frac{1}{1 + \frac{1}{2 + R}}

R = \frac{2 + R}{3 + R}

and hence

R^{2} + 2 R - 2 = 0

R = - 1 \pm \sqrt{3}

. As

R

must be positive we have the solution

R = \sqrt{3} - 1