Method of taking one item from the infinite set.
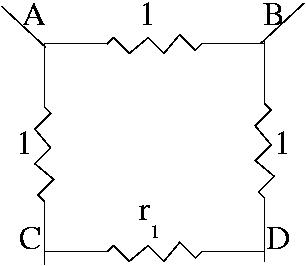
circuit with 4 resistances Denote the resistance of the infinite network by R. By removing just three resistances from the infinite circuit the resistance of the remaining infinite circuit is unchanged. The resistance between A and B is the same as the resistance between C and D cutting out the three resistances above. Hence r1 = R which gives
1
R
 = 1
1
 + 1
2 + R
and so
R = 2 + R
3 + R

giving the quadratic equation R2 +2R -2=0. Solving this equation, as R ³ 0 the solution is R=Ö3 -1 .
Method using a sequence and continued fractions.
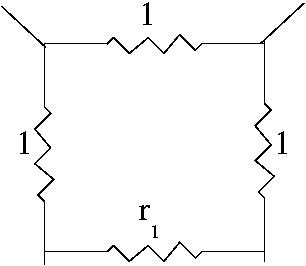circuit1 In this diagram r1 replaces the total resistance of the remaining network.

Taking R1 as the total of these 4 resistances:
1
R1
 = 1
1
 + 1
2 + r1
 .
So
R1 = 1
1 + 1
2 + r1



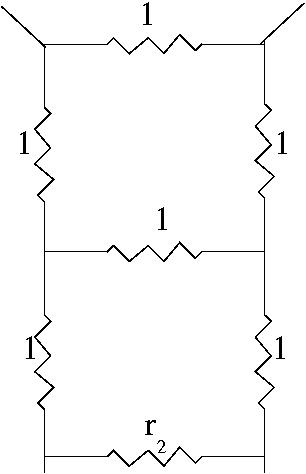
Now replacing r1 by 4 resistors where r2 replaces the total resistance of the remaining network as shown in the diagram we have
1
r1
 = 1 + 1
2 + r2
so r1 is replaced by
1
1 + 1
2 + r2
 .
Taking R2 as the total of these 7 resistances:
1
R2
 = 1 + 1
2 + 1
1 + 1
2 + r2
two rungs
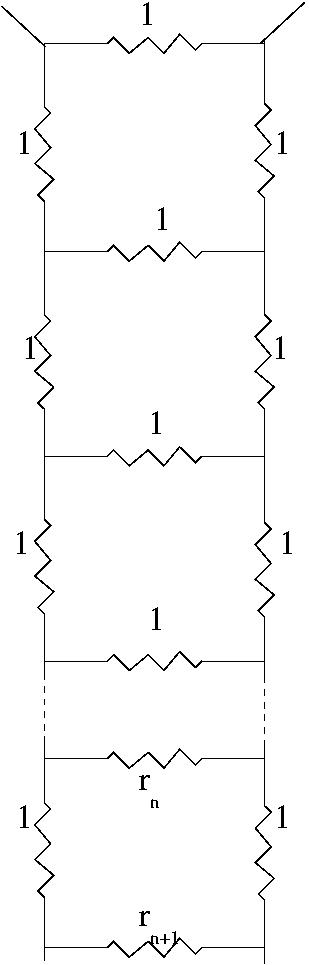infinite circuit Each time we add another 3 resistances to the network we replace rn by a resistance of 1 ohm in parallel with 3 more resistances of 1, rn+1 and 1 ohm in series such that
1
rn
 = 1 + 1
2 + rn+1
As the process continues indefinitely this gives the total resistance R in terms of the continued fraction
R = 1
1 + 1
2 + 1
1 + 1
2 + 1
1 + ...
 .
The periodic nature of this continued fraction enables us to calculate R as
R = 1
1 + 1
2 + R
so
R = 2 + R
3 + R

and hence R2 +2R-2 = 0 so R = -1 ±Ö3. As R must be positive we have the solution R=Ö3 -1 .