Suppose the first scale factor is
(so the second one is
).
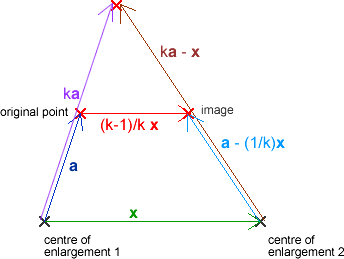
Let
denote the vector from the first centre of enlargement to
the second. Then the required transformation is a translation by the
vector
.
To see this, consider a single point on the flag. (If we show that the
required transformation for a single point is the given translation, then
the same will apply to the flag.) Let
denote the vector
from the first centre of enlargement to the point. Then the vector from the
first centre of enlargement to the image of the
point under the first enlargement will be
. The vector from
the second centre of enlargement to this image will be
, so the vector from the second centre of enlargement to the
final image will be
. So the vector from the initial point
to the final image will be
, as required.
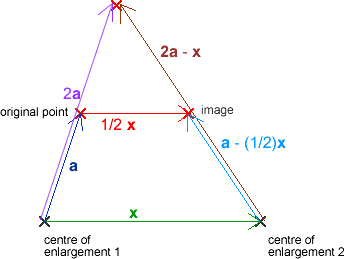
Here is a diagram with k=2:
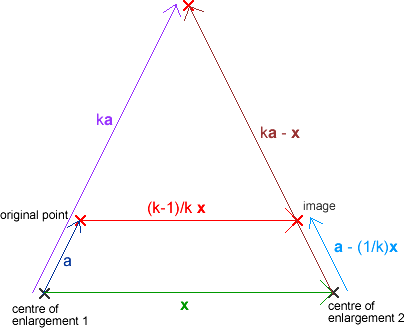
Here is the general diagram: