Calum from Woolmer Hill sent in his solution
to the first part of the problem:
Rotate the flag 180 degrees
around the point where the 2 lines meet.
Here is our explanation of the
transformations required in the general case of mirror lines at
any angle :
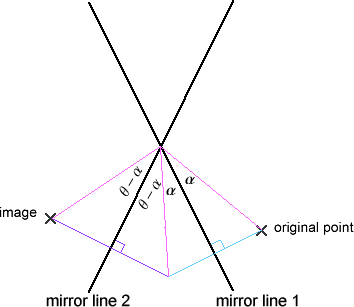
The resulting transformation is a rotation by
about the point
of intersection of the lines. If the direction of the angle
is from
the first line of reflection to the second, then the direction of rotation
is the same as the direction of
.
You should probably check that the same thing works if you reflect in the
further line first (remembering that this means the direction is reversed),
and if the flag is between the two lines.We just need to check the result
for a single point, because then every point will rotate by the same amount
and so the flag will remain intact (and will have rotated by the same amount).
The diagram says it all, really: the line segment joining the point to the
origin has rotated by an angle of
in the direction of
.