The flag is translated. The line through the two flags is
perpendicular to the lines of reflection. The distance between
the flags is twice the distance between the lines of reflection.
The translation is in the direction from line 1 to line 2.
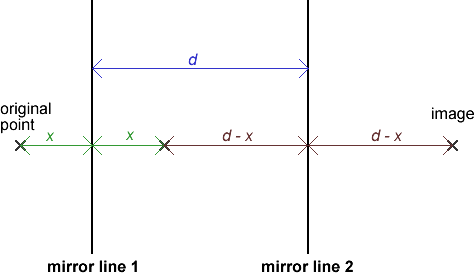
We may just consider a single point. We shall show that it is
translated to the right (assuming reflection in the left-hand
line first) by a distance equal to twice the distance between the
lines of reflection. This is sufficient to show that the above
result for the flag is true, because every point in the flag will
be translated to the right by the same amount.
The diagram says it all, really: the total distance moved by the point is
.
(Similar diagrams are needed to illustrate the cases when the flag is
between the lines of reflection and when the line nearer the flag is the
second line of reflection, but the principle is the same.)