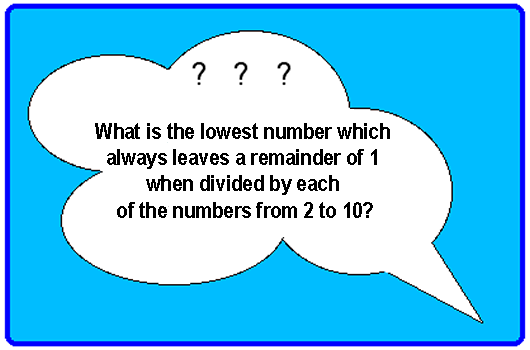A lot of teachers struggle with teaching division to children and
I have been thinking about this recently. I think there are a
number of factors contributing to this. Firstly, by the middle of
Stage 2 there is a huge range of levels of understanding of the
concept of division and secondly the concept itself can be
thought of as building on children's understandings of addition,
subtraction and multiplication. The spread of different levels of
understanding is likely to make any class "mixed ability" for
this topic. There are also difficulties with the written
algorithm. Altogether, it is a complicated picture.
Let us try to unravel this a little and find some interesting
problems that might help us to help our pupils. Let us start with
the different conceptions of division that are commonly used in
schools. We basically have three different ideas that we use with
children and we often switch between the languages of each
without thinking about the confusions this might cause for the
children.
Division is often introduced as "sharing" and this is certainly
one of the simplest approaches. We look at problems that involve
sharing a number of items between a number of different people.
We don't necessarily need to know how many items are in our
original pile or how many people we are sharing them between to
be talking about division in this way, and so this conception
doesn't easily lead to the representation of the situation in the
form of a mathematical expression such as
12¸4=3.
At this stage children need lots of experience with sharing
physical objects out and expressing what they are doing in words
and then in symbols. An interesting problem that works with this
idea is
Lots of lollies .
This was presented on the website as a Stage 1 problem with a
"three star" level of difficulty. This means that the maths
involved in solving it is within the Key Stage 1 curriculum and
that it is a very challenging problem at that level. I would be
happy to use it further up the age range as a vehicle for
re-visiting the topic of division and it would help to see
whether the children had developed some sound understandings of
ideas about sharing and remainders. On the website you can find
some different
solutions to the problem that children sent to us and these
make informative reading.
A second conception of division is that of grouping and this links to ideas
about successive subtraction. In this setting the problem is about how many
groups of a given number you can make out of a pile of items - "How many groups
of 3 there are in 12?"for instance. This links with ideas of
division as inverse multiplication and children can be offered plenty of
opportunities to explore patterns in the multiplication tables and to express
them in all the different ways that are possible, in words and in symbols.
For instance, our example of 3×4=12 generates a whole lot of sentences
and symbolic expressions: Three lots of four make twelve 4×3=12 Four lots of three make twelve There are three groups of four in twelve 12¸4=3 There are four groups of three in twelve 12¸3=4 If you share twelve things between three people they will have
four things each 12¸3=4 If you share twelve things between four people they will have
three things each 12¸4=3 It is important that children grasp the equivalence of all these different
expressions in order to develop their facility with division. In a
delightful book Williams and Shuard outline three stages in understanding
division as:
- Using grouping and sharing as different operations and solving problems
using concrete apparatus
- Relating sharing to grouping
- Using their knowledge of multiplication to deal with both types of
division by the same numerical procedure
These should be accomplished by working through the activities like the one above and
encouraging children to communicate with one another about their
understanding. Working on from using known facts, the next problem arises with the written
algorithms for division. Unlike the other standard algorithms for addition,
subtraction and multiplication, the standard algorith for division is
worked from right to left and the setting down seems totally different. Despite much
advice about not introducing written algorithms too early, many children
meet it before they are ready to understand it and without being given enough
chance to develop their own strategies for dividing large numbers. Stuart
Plunkett's comment made way back in 1978 still rings true: ``Children should be helped to acquire sensible methods for
calculating''
The value of informal jottings to record division calculations has been
outlined by Julia Anghileri and she shows some interesting analysis in the
book ``Teaching Number Sense''. Before children embark on any formal
recordings using the standard algorithm for division they need plenty of
familiarity with tables and number patterns in them as well as practice
with mental strategies such as chunking, doubling and halving. All of these activities do require a lot of practice and experience but once
you are confident that your class have had a good grounding in these areas,
why not try some of these problems?
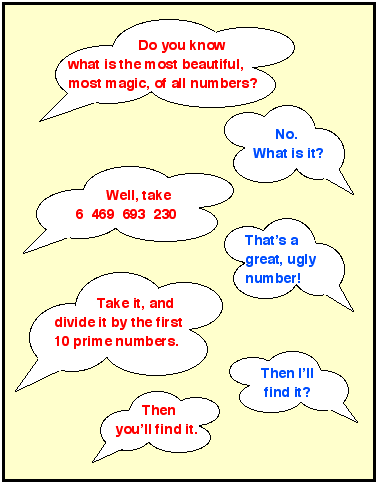
This problem offers a lot of practice of division as well as
revision of ideas about prime numbers in a situation in which
children want to get to the answer -much more fun than a page
of 'sums' but just as much practice. It originally appeared on
the website as a Stage 2 one star problem so the level of
challenge should mean that children can make a start on it
fairly easily. Those who find it easy could be encouraged to
invent their own similar problems which will give them practice
with multiplication as well.
Here is another at the same level:
Again there is plenty of opportunity to practise division and
multiplication as well as the chance to invent other similar
problems. There are plenty of other problems too such as
Skeleton which is a puzzle about missing numbers in the
written algorithm or
Oh! Hidden Inside which explores factors and multiples.
American Billions should prove a challenge for the highest
of fliers at Stage 2 as well as their teacher! Happy hunting
and I hope that the next time you are faced with the difficult
task of teaching division, you and your class will enjoy it and
even find it easy.
References:
Anghileri, J. (2000) Teaching Number Sense. Continuum.
Plunkett. S, (1979) 'Decomposition and all that rot'.
Mathematics in School 8(3), pp. 2-5.
Williams, E. and Shuard, H. (1994) Primary Mathematics Today.
Longman