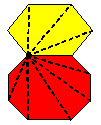
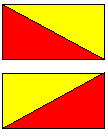
| The sequence of five steps in this proof starts with 'adding' polygons by glueing two polygons along an edge and showing that if the theorem is true for two polygons then it is true for their 'sum' and 'difference'. |
 |
| The next step is to prove the theorem for a rectangle, then for the triangles formed when a rectangle is cut in half by a diagonal, then for the general triangle (labelled in the diagram below), and finally for any planar polygon because it can be built up from 'adding' triangles. Although the proof is long it is simply a matter of counting points. |  |
| (4) Prove that Pick's Theorem holds for the general triangle shown in this diagram. (5) Prove that Pick's Theorem holds for any planar polygon. |