Now suppose the common edge of $P_1$ and $P_2$, which joins 2 boundary lattice points of $P$, includes $n$ other lattice points which become interior points of $P$ so that $i=i_1+i_2+n$. Now lattice points $A$ and $B$ at the ends of the common edge of $P_1$ and $P_2$ belong to the set of points on the perimeters of both $P_1$ and $P_2$ so we subtract 2 so they are not counted twice to give $p=p_1-n+p_2-n-2$.

Now

${\displaystyle \mathrm{area}(P)=\mathrm{area}(P_1)+\mathrm{area}(P_2)}$

so equivalently

${\displaystyle \begin{array}{cc}\multicolumn{1}{c}{F(P)+(i+\frac{1}{2}p-1)}& =F(P_1)+(i_1+\frac{1}{2}{p}_1-1)+F(P_2)+(i_2+\frac{1}{2}{p}_2-1)\\ \multicolumn{1}{c}{}& =F(P_1)+F(P_2)+(i_1+i_2)+\frac{1}{2}(p_1+p_2)-2\\ \multicolumn{1}{c}{}& =F(P_1)+F(P_2)+(i_1+i_2+n)+\frac{1}{2}(p_1-n+p_2-n-2)-1\\ \multicolumn{1}{c}{}& =F(P_1)+F(P_2)+(i+\frac{1}{2}p-1)\end{array}}$

and so

${\displaystyle F(P)=F(P_1)+F(P_2).}$

So, if Pick's function is zero for any two of these polygons it must be zero for the third. This means that if Pick's Theorem holds for any two of these polygons it must hold for the third.

(2) For the rectangle $R$ with vertices $(0,0),(a,0),(a,b)$ and $(a,b)$ there are $(a-1)(b-1)$ interior points and $2a+2b$ points on the perimeter. Hence Pick's function for this rectangle is given by:

${\displaystyle F(R)=\mathrm{ab}-[(a-1)(b-1)+\frac{1}{2}(2a+2b)-1]=0.}$

(3) If the rectangle $R$ is split into two equal triangle by a diameter then each triangle has the same area and the same number of interior points and points on the perimeter and hence Pick's function must take the same value for each triangle. By parts (1) and (2) Pick's function must be zero for such triangles.

When a polygon with vertices at lattice points is translated so that the image has vertices at lattice points there is no change in area, or in the number of interior lattice points, or in the number of lattice points on the perimeter. Hence Pick's function is zero for all rectangles and for right angled triangles, with vertices at lattice points, which have sides parallel to the axes.

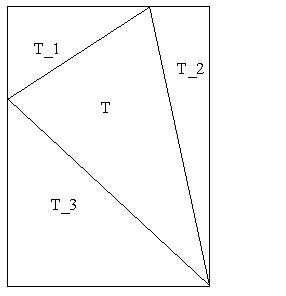
(4) A general triangle, whose vertices are lattice points, can be enclosed in a rectangle by drawing lines parallel to the axes as shown in the diagram. By parts (1) and (3), as Pick's function is zero for the enclosing rectangle and for $T_1$, $T_2$ and $T_3$, it is also zero for the general triangle $T$. (5) By part (4) Pick's Theorem holds for a general triangle which has integer lattice points. Any planar polygon can be split into triangles. The argument in Part (1) can be extended inductively for any number of triangles which have common edges and together make up a planar polygon. Hence Pick's Theorem is true for all planar polygons.