On the twelfth day of Christmas, my true love gave to me.. .

How many gifts?
But that's easy; all you have to do is add up the numbers from one to twelve.

That sounds easy, but what if the last line had been... fifty drummers drumming ?
Isn't there a better way than huddling over your calculator?

And a partridge in a pear tree...

On the fifth day

1 + 2 + 3 + 4 + 5 = 15

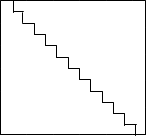
gifts are given. We can visualize this as

15

squares arranged into the shape of a staircase;

1

square on top of

2

squares on top of

3

squares etc.

Two of these staircases can be placed together to form a rectangle. The stair shape is half the area of the rectangle, which is:

\frac{5 \times (5 + 1)}{2} = 15

For the twelfth day we can repeat the process and end up with a new rectangle, as shown on the right. The rectangle is

12

12 + 1 = 13

. We can now say:

1 + 2 + 3 + . . . + 12 = \frac{12 \times (12 + 1)}{2} = 78

So the true love gets

78

gifts on the twelfth day of Christmas.

How many gifts arrive on the $n$ th day?

The same argument applies and we would end up drawing a rectangle that was $n$ squares high and $n + 1$ squares wide. We would end up with:

$1 + 2 + 3 + . . . + n = \frac{n \times (n + 1)}{2}$

Four turtle doves...

That's all well and good but what if the true love went overboard on the whole gift front?

Instead of two turtle doves, he gave four;

instead of three French hens he gave nine ...

More precisely, if instead of giving $n$ gifts on the $n$ th day, $n \times n$ (normally written as $n^{2}$ ) gifts are given, then what?

Now on the twelfth day there would be

1 + 4 + 9 + 25 + \dots + 144

gifts.

Is it time to huddle over our calculator now?

Not quite yet, we can visualize the number of gifts on the third day, for example as $1$ cube on top of $4$ cubes on top of $9$ cubes arranged as in Figure A.

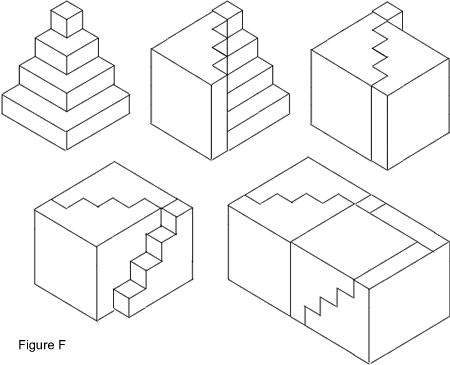
Now treat the object in A as a single building block. If you put two of these building blocks together you get the solid in Figure B.

Adding another building block you get the solid on the left in Figure C. The picture on the right is just a different view of the solid shown on the left.

Figures D and E show two copies of the solid made from three building blocks separately (D) and then placed together (E).

Now what is the point of all this?

Well the task is to work out how many cubes are inside our building block, we can do it two ways.

By direct counting we get:

$1 + 4 + 9 = 14$ .

But we also have shown that six of our building blocks can be arranged into the solid cuboid in Figure E. So, how many cubes are there in Figure E?

Well the cuboid is $3$ cubes high, $4$ cubes wide and $7$ cubes long and the cuboid contains $6$ of our building blocks.

So the volume of our building block is:

$1 + 4 + 9 = \frac{3 \times 4 \times 7}{6} = 14$

Now here's a question:

Would the construction have worked if our building block had more layers, e.g. $1$ cube on top of $4$ cubes on top of $9$ cubes on top of $16$ cubes?

We can repeat the process, but this time starting with a block with four layers.

The final solid in Figure F is now a cuboid that is $4$ cubes high, $5$ cubes wide and $9$ cubes long and the cuboid contains $6$ of our building blocks.

So in this case the volume of the building block is

$1^{2} + 2^{2} + 3^{2} + 4^{2} = \frac{4 \times 5 \times 9}{6} = 30$

By staring at the images, I hope you would agree that we can start with a building block that has any number of layers and that following the same construction we would end up with a cuboid that is $n$ blocks high, $n + 1$ cubes wide and $2 n + 1$ cubes long and contains $6$ our of building blocks.

So then the volume of the building block would be

$1^{2} + 2^{2} + 3^{2} + \dots + n^{2} = \frac{n \times (n + 1) \times (2 n + 1)}{6}$

So our overzealous gift giver would have bestowed

$\frac{12 \times 13 \times 25}{6} = 650$

gifts on his true love on the twelfth day.

N.B. You can find an algebraic proof of this result in the article " Mathematical Induction " on the site.

Twenty-seven French hens ...

You may now have an inkling as to where this is heading:

what if instead of two turtle doves, he gave eight

and three French hens became twenty-seven?

Demonstrations of the following result in this article can be found but are not included here, for example you can look at the problem " Picture Story " .

1^{3} + 2^{3} + \dots + n^{3} = (1 + 2 + 3 + \dots n)^{2}

A very pleasing result which means that ...
On the twelfth day our exhausted distributor of gifts would have dispensed:

1^{3} + 2^{3} + \dots + 12^{3} = (1 + 2 + 3 + \dots 12)^{2} = 6048 gifts

Two hundred and fifty-six calling birds and more ...

So why stop there?

Well, if you are feeling a bit taxed and want to stop here, I think I have given you enough to think about.

For the rest of you intrepid explorers who want to carry on to the summit, for a whole number

n

and

m

..., go to the notes for more and more and more....