This solution was sent in by Chris who is about to start at Oxford University.

My instructions will all be in the form draw $([a_1,a_2...,a_n],[\theta_1,\theta_2,...,\theta_n])$ and my angles will be in degrees.

There are three types of graph; one that is periodic, one that shoots off and grows without bound, and one that stays within a certain space but is not periodic.

Those of the third type are the easiest to define mathematically. For example draw $([20],[19\pi])$ which appears to start drawing a pentagon but does not quite connect up, instead continuing to loop round taking a slightly different path each time.

Graphs which stay in a closed space but are not periodic occur simply when $S_{\theta} = \theta_1+\theta_2+....+\theta _n$ is not rational . This is because, after turning through each angle once, the pen has turned through $S_{\theta}$ degrees. If $S_{\theta}$ is not rational then no matter how many times the instructions are carried out, the pen will NEVER face the same way twice so cannot be periodic and cannot continue in a straight line overall.

So how can we be sure they only exist within a finite area? If we again consider the position of the pen after it has executed some instructions such that it is on the starting point $a_0,\theta_0$ again then it has moved distance $a_x$, which is zero 'vectorally', and turned through angle $S_\theta$ which is irrational. Now draw $([a_x],[S_\theta])$ which will always curl round on itself and would obviously be restrained to a finite area so therefore the whole graph must also be within a finite area.

The second set of graphs that shoot off and grow without bounds are created when some instructions have been carried out such that $([a_1],[\theta_1])$ are the next instructions, and the pen is some distance greater than zero away from the starting position and facing the same way as when it started. The pen has now travelled distance $a_x \neq 0$ and since it is facing the same direction will carry on in a straight line as long as the instructions are followed, i.e. the instructions will follow two rules:

1) $k\times S_\theta/T_\theta = 0 {\rm mod}\ 360$
where $S_\theta$ is the sum of all the angles, $T_\theta$ is the total number of angles and $k$ is the lowest common multiple of the (number of length instructions) and the (number of angle instructions).
2) After $k$ steps, the total distance moved is greater than zero.

To calculate this, call $\theta_n$ the angle the pen is facing after $n$ steps. If $a_1\cos \theta_1+a_2\cos \theta_2 +...a_k\cos \theta_k \neq 0$ or $a_l\sin\theta_1+a_2\sin\theta_2+...a_k\sin\theta_k \neq 0$ then, after $ k$ steps, the total distance moved is greater than 0.

The set of periodic graphs issubject to two rules:

1) $S_\theta$ is rational.
2) If $k\times S_\theta = 0 \ {\rm mod}\ 360$ then the total distance moved after $k$ steps is 0.

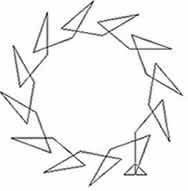
In the first diagram the total turn for each cycle is 330 and as $12\times 330 = 11\times 360$ the path returns to the starting point after 12 repetitions of the cycle and a total turn of 11 complete revolutions. The program in Logo is:

repeat 12 [fd 50 rt 40 fd 50 rt 130 fd 50 rt 160]

(where fd 50 means go forward a length 50 units and rt 40 means turn right, i.e. clockwise, through an angle of 40 degrees)

Adding the three vectors which make up a cycle (e.g

\vec{AB} + \vec{BC} + \vec{CD}

) is a simple exercise intrigonometry.

The problem reduces to the same problem as in the Spirostars case because, joining the starting points of successive cycles gives line segments of constant length with a constant angle of turn of 30 degrees between each line segment.

In this diagram the total turn for each cycle is 450 degrees. As

4 \times 450 = 5 \times 360

the path returns to the starting point after 4 repetitions of the cycle and a total turn of 5 revolutions. The program is:/par repeat 4 [fd 100 rt 90 fd 10 rt 90 fd 20 rt 90 fd 50 rt 90 fd 25 rt 90 ]

In this case by joining the starting points of successive cycles we get line segments of constant length with a constant angle of turn of 90 degrees between each line segment.

In this diagram the turn for each cycle is 200 degrees. As

9 \times 200 = 5 \times 360

the path returns to the starting point after 9 repetitions of the cycle and a total turn of 5 revolutions. The program is:

repeat 9 [fd 100 rt 120 fd 200 rt 80]

In this case, by joining the starting points of successive cycles we get line segments of constant length with a constant angle of turn of 40 degrees between each line segment.

In the case where the graph continues off to infinity the vectors joining the starting points of successive cycles are all in the same direction so the patterns repeat themselves over and over again along a parallel strip.