Working in degrees, if q divides 360 then the shape will be a regular polygon. Else if q is rational, the shape will be a star. If q is irrational then a 'donut' shape will eventually be drawn, i.e. a star with infinitely many points.

Consider theta being irrational. No matter how many turns are made, the pen will never be pointing in the same direction so cannot repeat its path.

To complete the solution to this problem, consider the diagram:

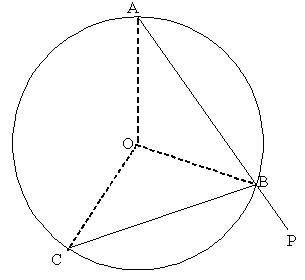
First think: 'why do the points lie on a circle?' We should not take for granted that they do so we must first prove it. Draw the perpendicular bisectors of the line segments AB and BC, then the intersection of the perpendicular bisectors is equidistant from A, B and C and thus it is the centre of the circle with AB and BC as chords. All the perpendicular bisectors of the line segments in the path will meet in a single point O equidistant from the endpoints of the line segments. Therefore all the line segments are chords of a single circle with centre O. The angle of turn between the equal chords AB and BC in the path is ÐPBC = q. Triangles AOB and BOC are isosceles and ÐOAB = ÐOBA = ÐOBC = a. Then (using angles on a straight line and angles in a triangle) q = 180 - 2a = ÐAOB.

Consider radii drawn from the centre to the ends of n consecutive chords in the path....

Now can you prove that the path is closed if and only if q is a rational multiple of 360 degrees? Consider radii drawn from the centre to the ends of n consecutive chords in the path. The sum of angles between the radii is equal to the total angle turn nq so the path is closed if and only if the total angle turn is an integer multiple of 360 degrees, that is if and only if nq = 360m or, equivalently q is a rational multiple of 360 degrees.

So consider q = 360 ^p/_q where p and q are positive integers and p < q. If the angle of turn is more than 360 degrees, complete revolutions can be discounted, so effectively

q = 360

p* q

produces the same path as q = 360 ^p/_q where p* º p mod q.

If p is a factor of q, (say q = kp) then the path is a regular k sided polygon because the total angle turned when k chords are drawn is

k ×

360 k

= 360

degrees.

If p and q are not coprime then sp=tq for some integers s and t so that the total angle turn with s chords is s × 360^p/_q = 360t which is an integer multiple of 360 degrees so the path is a star with s points. If p and q are coprime then the path is a q pointed star.