Happy Numbers were introduced in
this problem from June 1997.
I was first shown Happy Numbers twenty years ago. It works like
this:
Chains of numbers are made. The first number in the chain is
split into individual digits, each digit is squared and the sum
of these squares becomes the next number in the sequence, and so
the process continues; splitting, squaring and adding.
For example, starting with 35 the next number is 34, that's 9 +
25, the number after 34 is 25, followed by 29, 85 and so on.
Explore this process for yourself to see what happens.
Do numbers just get larger and larger, or is there a limit?
Do numbers eventually map back to themselves?
Using a spreadsheet for mapping
sequences of this kind
Sometimes a mathematical situation seems to have no particular
purpose but, if our curiosity is excited, and our minds become
energised, then exploring a situation's possibilities may reveal
an interesting structure or lead us to invent a technique that
could be useful elsewhere. That is what happened for me with this
investigation. I should admit that the Happy Numbers
investigation itself has never done much to arouse my curiosity.
When I found answers, my response was "OK, now I know. So what?"
But the investigation did lead me to try out an Excel function
which looked up results I had already calculated, and that was a
worthwhile discovery.
Putting Excel to work
As always, the main value of the spreadsheet when investigating a
mathematical situation, is to give results quickly and easily, so
that as much of my attention as possible is available to think
about any patterns or connections I notice.
When I first explored Happy Numbers I didn't use a spreadsheet.
Actually twenty years ago spreadsheets were strange and new to
most people. In some ways that was a good thing. Using a computer
can frequently become the automatic choice. When we realise we
have become automatic in our response to a situation it can often
be helpful to pause and try out the options; at least in our
imagination.
Twenty years ago, in my pre-spreadsheet days, I sat for a bit,
thought about the process I was being invited to explore, tried
out a few calculations, started recording some results, and so
on. I still usually start work this way.
After a little while I realised that I was spending too much time
calculating and not enough time thinking about what was happening
in the process. I did notice that the order of the digits was
unimportant, that starting at 35 or 53 was really the same thing
apart from the first number. I also invested ten minutes, away
from the main task, to made a table of results so that I could at
least stop doing all of the individual calculations and record my
results faster.
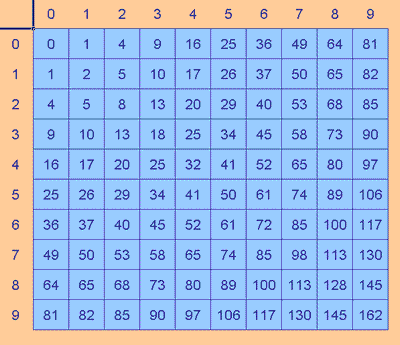
I produced the table back then by doing my own calculations,
except for the symmetric values of course. Now I would very
likely use a spreadsheet for a table of results from a function
of two independent variables.
Click
here to see how to do this.
The table of results also helped in another way. It helped me see
that all two-digit numbers mapped onto one- or two-digit numbers,
except those that mapped onto 100, 106, 113, 128, 130, 145, or
162, but each of these immediately map back to a two-digit
result, so the set has closure.
It is also worth pausing to see what happens to numbers with
plenty of digits (they always reduce in size), and to understand
why that happens.
The three-digit number which produces the largest next value is
999, and this maps to 243, so all three-digit numbers map to
three-digit numbers until they fall into the two-digit set
discussed above.
The four-digit number which produces the largest next value is
9999 which maps to 324, so all four-digit numbers map to numbers
with less than four digits.
I said earlier that the Happy Numbers problem did make me think
about how to use a spreadsheet in a new way: to look up results I
had already calculated.
Here's how I did that:
Happy Numbers with
VLOOKUP
Although the square table was useful when I had to fill in the
answers myself, because it saved me doing separate calculations
for both numbers in a pairs like 35 and 53, once a spreadsheet is
doing the calculations this saving is not of much value.
So I produced a table that had the numbers from 1 to 200 in the
first column, split these numbers into individual digits, which
were then squared and added up.
Here's the Excel file for the Happy Numbers mapping .
Isolating Digits
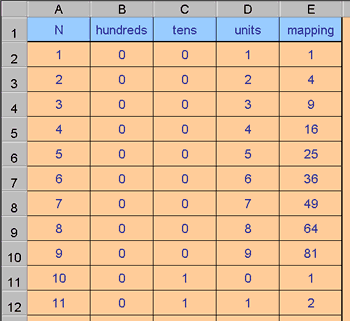
In the Excel file "Happy Numbers mapping" column A contains the
value to be mapped, columns B, C, and D contain the individual
digits, and column E contains the mapping.
The following explains how the digits are isolated.
You need to understand that the INT function takes the integer
part of a value and ignores the rest. INT of 3.845 is just 3.
B2 calculates the number of hundreds using the formula:
=INT(A2/100)
A2 was the original value, dividing it by 100 and taking just the
integer part of this result reports the number of hundreds in the
original number.
For example: 374 divided by 100 is 3.74 whose integer part is 3,
the hundreds digit.
C2 calculates the number of tens using the formula:
=INT(A2/10)-10*INT(A2/100)
INT(A2/10) calculates the number of tens. For the example of 374
this would be 37.
INT(A2/100) calculates the number of hundreds, 3, as already
explained.
So 37 minus 10 lots of 3 gives the result 7, the tens digit as
required.
D2 contains the formula: =A2-10*INT(A2/10)
INT(A2/10) is the number of tens, 37 in the example.
So the original number minus 10 lots of the number of tens, 374 -
370, gives 4, the required units digit.
Once I had these basic results available, Excel could look these
up as each sequence was created using starting numbers 1 to 200 .
Click here to see the Excel file Happy Numbers .
Click here to see the same Excel file with conditional formatting used to
highlight the structure .
Using Conditional Formatting makes values of interest easier to
see.
Click
here to look at notes on conditional formatting.
When to use the LOOKUP
technique
What made this problem different from some other sequence work
was that the mapping rule was not a single, simple formula to
enter into a spreadsheet cell.
Consider a very different example:
I can find one approximate solution to the equation x2 - 7x + 9 = 0, capable of unlimited refinement, by using the sequence
mapping rule:
7 - ( 9 divided by the previous value)
It's easy to tell the spreadsheet to take a number, divide 9 by
that number, and subtract that result from 7.
Happy Numbers was harder because the digits needed to be
separated first.
Although this could have been part of the Excel formula, it
would have been a lot to bundle into a single cell, and the
risk of error increases.
Done using the Lookup command instead, the process is easy to
understand, the results referred to are laid out in an
easy-to-follow fashion and the whole process remains
transparent.
For this method it was also necessary that the results formed a
closed set. Each result leads to another result from that same
set.
This kind of structure helps to keep a process clear, making
interesting relationships easier to spot, and explain.