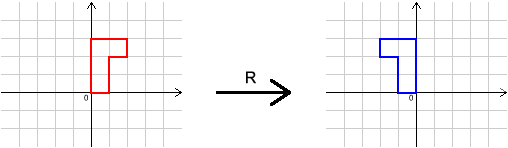
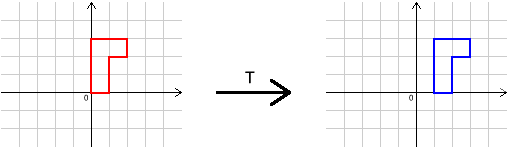
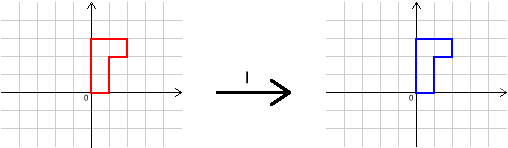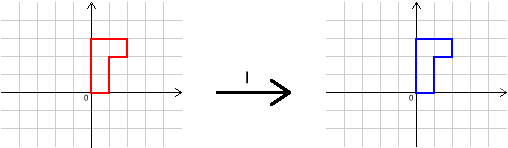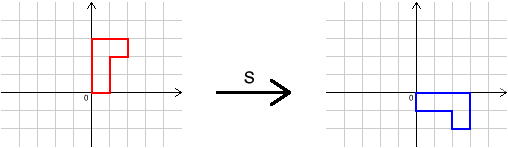In this problem, we shall use four transformations,

I

R

S

and

T

. Their effects are shown below.

We write

R^{- 1}

for the transformation that "undoes"

R

(the inverse of

R

), and

R S

for "do

R

, then

S

".
We can write

T

followed by

T

T T

T^{2}

, and

T

followed by

T

followed by

T

T T T

T^{3}

and so on.
Similarly, we can write

S^{- 1} S^{- 1}

S^{- 2}

and so on.

Try to find simpler ways to write:

$R^{2}$ , $R^{3}$ , $R^{4}$ , ...

$S^{2}$ , $S^{3}$ , $S^{4}$ , ...

$T^{2}$ , $T^{3}$ , $T^{4}$ , ....

What do you notice?
Can you find a simpler way to write $R^{2006}$ and $S^{2006}$ ?
Can you describe $T^{2006}$ ?

Let's think about the order in which we carry out transformations:
What happens if you do $R S$ ? Do you think that $S R$ will be the same? Try it and see.
Is $T^{2} R$ the same as $R T^{2}$ ?
Is $(R T) S$ the same as $S (R T)$ ?
Try this with some other transformations.

Does changing the order
       always
       sometimes
       never
produce the same transformation?

Now let's think about how to undo $R S$ . What combination of $I$ , $R$ , $S$ , $T$ and their inverses might work? Try it and see: does it work? If not, why not? Can you find a combination of transformations that does work?
How can you undo transformations like $S T$ , $T R$ and $R S^{2}$ ?

This problem is the middle one of three related problems.
The first problem is Decoding Transformations and the follow-up problem is Simplifying Transformations .