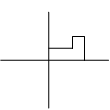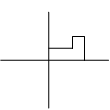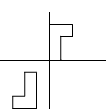We received many correct solutions describing each of the transformations. Well done Rahel from Dartford Grammar School for Boys, Harry from Culford, Dominic, Ellie, Finn and Max from Brenchley andMatfield Primary School, Jannis from Long Bay, Ben from the Perse School and Emilio from St Peter's College.

However, the second part caught almost everyone out: since it looked like the first four transformations were "undone" by their inverses, most people thought that the string of transformations returned the original shape back to where it started.

Only Emilio managed to work out that this was not the case:

From the first figure, it can be seen that

S

rotates the figure

90^{\circ}

clockwise round (0,0).

The second figure shows $S^{- 1}$ then $R$ .
Because $S$ = $90^{\circ}$ clockwise, $S^{- 1}$ must equal $90^{\circ}$ anticlockwise.
$S^{- 1} R$ rotates the figure $90^{\circ}$ anticlockwise and then reflects it vertically.
Therefore $R$ reflects the figure in the vertical axis.

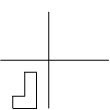
The third figure has $R$ then $T$ .
The final figure finishes one square right after performing $R$ .
Therefore $T$ must translate the figure one square right.

By doing $R$ to the original figure (fourth example), the shape ends up the same as the final product of $R$ and $I$ .
Therefore $I$ does nothing.

To solve the final part, we need to work through each stage individually.

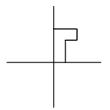
original shape

$R$ reflects the figure vertically.
$S$ rotates it 90 degrees clockwise.
This leaves the figure like this:

T

translates the figure 1 right:
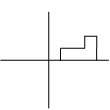
translated figure

I

will do nothing.

R^{- 1}

reflects the figure again because inverse reflections are the same as the original reflection.
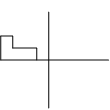
reflected shape

S^{- 1}

rotates the figure

90^{\circ}

anticlockwise:
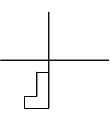
rotated figure

T^{- 1}

will translate the figure left one square.

I

does nothing, so

I^{- 1}

will do nothing.

Therefore a rotation of $180^{\circ}$ round (-0.5, -0.5) will have the same result as $R S T I R^{- 1} S^{- 1} T^{- 1} I^{- 1}$

Well done Emilio.

Editor's note:

R S T I I^{- 1} T^{- 1} S^{- 1} R^{- 1}

would leave the original shape unchanged since the inverse transformations would be applied in the reverse order, "undoing" the last transformation first (and the first one last).

(If I put on my t-shirt and then put on my jumper, I "undo" this by taking my jumper off first and then my t-shirt.)