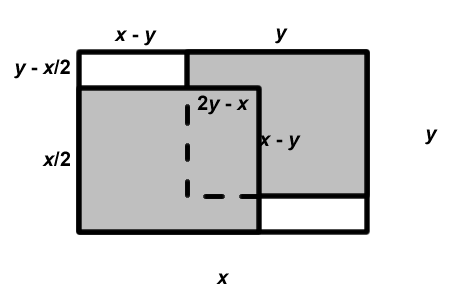
1:1

Let the sheet of paper have length

x

and width

y

. Then the uncovered area consists of two congruent rectangles of length

x - y

and width

y - \frac{1}{2} x

. So the uncovered area is

2 (x - y) (y - \frac{1}{2} x)

, that is,

(x - y) (2 y - x)

The area covered twice is a rectangle of length $y - (x - y)$ , that is, $2 y - x$ , and width $\frac{1}{2} x - (y - \frac{1}{2} x)$ , that is, $(x - y)$ . So the area covered twice is also $(x - y) (2 y - x)$ .