Suzi from Perth had some good answers
and excellent reasoning
Question : If this sector had a radius of 10 units what would
the area be?
I need to calculate
of the whole circle :
of p times 102 is 236 sq.units correct to 3 significant figures
Question : If the sector is made into a cone by closing up the gap, what will be the base radius for that cone?
of the full circumference of the large incomplete circle is used to make the complete circumference of the cone base.
I then realised that it isn't actually necessary to calculate these lengths.
For every circle the diameter and circumference keep their ratio to each other (that's what p is) so the new diameter is just
of the old diameter, because the new circumference is
of the old circumference, so the cone's base radius is 7.5 units.
Question : If the cone now suffers a horizontal cut which
removes its top, reducing its height by half, how much curved
surface area remains?
Think of it like this :The original whole sector now has its
centre missing.

The original and the removed sector are similar shapes with a line ratio of 1:2
So the area of the original sector must be four times the area of the removed sector (that's just squaring the line ratio) which means that the curved surface area of the lower remaining part of the cone is
of the sector already calculated.
And that comes to 177 sq.units (3 sf)
Dean from Cheadle & Marple College
used reasoning like this to get a general formula for the area of
a whole cone's curved surface :
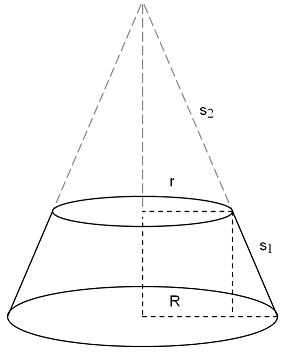
Starting with a cone whose base radius is r and slope length is s.
The curved surface is a sector from a circle with radius s. The sector fraction is found by comparing the cone base circumference with the circumference of a circle whose radius is s.
So the fraction is r/s ,the whole area was p s2 and that simplifies to psr for a cone's surface area not including the base.
Dean then produced a general formula for the
area of a frustum's curved surface.
R and r are the radii top and bottom for the frustum and s is
the slope length.
This involves some fiddling with the algebra but it's a nice
result when you have done it.
What's needed is the difference in surface area between the
two cones.
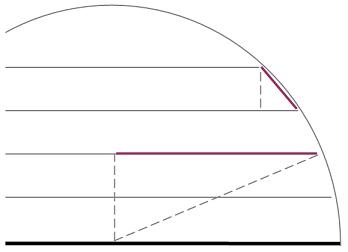
From the
diagram you can see that a length s2 will be involved which isn't
very convenient because s2 isn't a length you can measure somewhere
on the frustum. However if you notice the similar triangles present
in the diagram you can find a connection between s1, s2, r and R And
from that s2 can be expressed as a formula using only s1, r and R
This formula can replace any s2 in the area expression and when you
tidy things up (not that quick to do) it reduces to the pleasantly
simple p s(r+R)
Next Dean explained that when the
apple (sphere) is approximated to a stack of frustums (he used
five) you can find all the lengths you need so that you can use
that formula for the area of the curved surface on each frustum
in turn, then for m a total.
If you know how thick you've chosen the frustums to be you
know the height.
The radius of the sphere you know and so applying Pythagoras'
Theorem it is possible to find any radii lengths required.
Using Pythagoras also to find the slope lengths each time by
using the thickness of the frustum and the difference between the
top and bottom radii.
Here's part of Dean's spreadsheet and his
comment on the result.
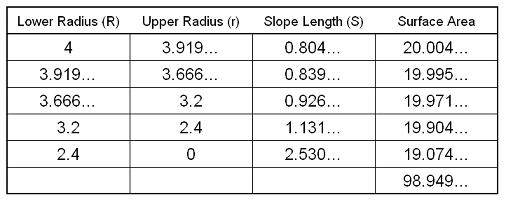
Thus the amount of peel of an apple of diameter 8cm is 197.899
(3sf) after doubling the hemisphere result from the sheet.
If this answer is
compared to the result from using the equation for surface area of
a sphere which is 4 p r2 and gives 201.062 . . . it can be seen that there is
a percentage error of 1.57
If 50 frustums are used the percentage error drops to
0.02%.
Which leaves us pleasantly curious about
that formula Dean found which calculates the surface area for a
sphere.
If I know the surface area for a sphere of unit radius I can say that the surface area for a sphere of radius r would be r2 times as much so it's the right kind of formula. I wonder if we can verify that 4p multiplier.
Continuing that line of thinking. If I know the volume for a sphere of unit radius I can say that the volume for a sphere of radius r would be r3 times as much. That tells me what type of formula to expect now perhaps I can use that spreadsheet technique to find the volume of a sphere with unit radius. I wonder if it's a nice number of p like the surface area?