This is a very practical challenge which you may want children to
investigate over a series of lessons or even during an entire
day. It will help to reinforce their understanding of properties
of cuboids and they will be practising calculating volume.
However, this is also a great opportunity for you to emphasise
the power of using visualisation to solve a problem and of
working systematically.
It will be necessary to introduce this investigation to the whole
group in a practical way to make sure that they understand what
the challenge is. Having a box of the correct size already made
will be helpful - of course you could alter the dimensions you
work with to suit some boxes you have to hand. You could begin by
making a small cuboid out of cubes and asking the children to
estimate how many of your cuboids might fit in the box. Try a few
examples like this, using bigger cuboids each time so that it
becomes harder to tell whether two will fit in or not. End with
an example which is obviously too big to be fitted in the box
more than once. You can then introduce the question itself.
We would recommend that children work in pairs or small groups
for this activity. The quality of discussion will help to inform
your assessment of the children and it would be useful to bring
the whole class together at suitable intervals to talk about
their ideas.
Well what I've seen often goes something like this:
1st attempt - after some initial thoughts, it needs to be a little bigger than
half, so let's put a cuboid onto the base and let it be half (plus 1) high!
So we get 12cm x 8cm x 6cm which has a volume of 576 cm3.
2nd attempt - a similar idea but what about a little bigger than half but
up against the narrow side, so let's put a 7cm x 8cm x 10cm cuboid in, which
has a volume of 560 cm3.
3rd attempt - well there will be a third one in this way that goes
against the long side, so we'll put in a 12cm x 5cm x 10cm cuboid which has a
volume of 600 cm3.
These diagrams show these three attempts:
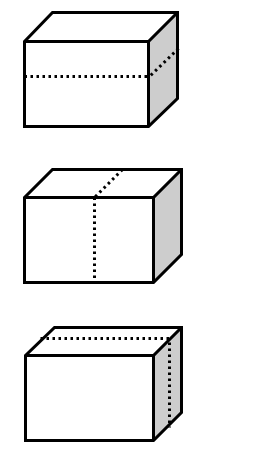
4th attempt - can we combine two of these previous ideas to make something a
bit bigger than a quarter of the volume of the box? We'll try a
7cm x 8cm x 6cm with a volume of 336 cm3 that's much better. BUT can we fit
another one in?
Here's a bit of extension work.
If you work on the first ideas of taking half of one of the
dimensions and adding 1, and then go on to combining two
dimensions and finally three there are 7 possibilities. Moving
away from the original challenge we can investigate these 7
cuboids.
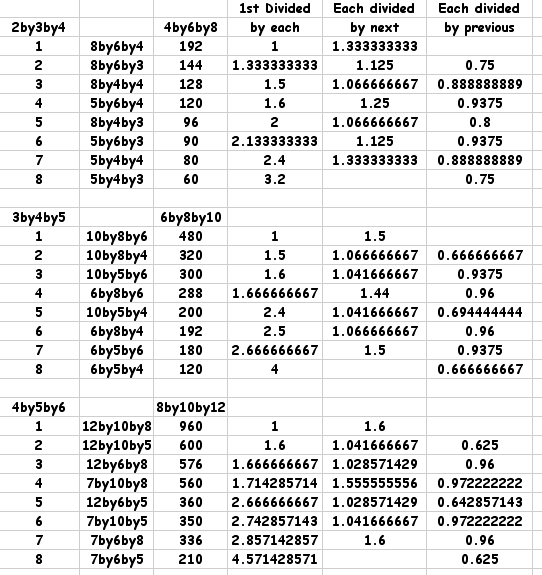
I've been exploring three different sizes of boxes, 4 x 6x 8, 6 x
8 x 10, and 8 x 10 x 12 - each being double a set of consecutive
numbers.
The next stage was to look at the volumes of each of the cuboids
together with the boxes they were to go into making 8
altogether.
Then I explored various divisions.
This kind of exploration developing from a practical situation
can lead some of the more able pupils into unexplored areas of
number patterns!