Thank you Hutch from Park College and Andrei from Tudor Vianu National College, Bucharest for your solutions to this problem.

Reflection in two parallel axes gives a translation Reflection in line A maps foot 1 to foot 2.\\ Reflection in line B maps foot 2 to foot 3.\\ The combination of these 2 reflections is a translation perpendicular to the mirror lines by twice the distance between the two mirror lines. \par \par \par \vskip 2 cm {\bf Reflection in two intersecting axes gives a {\it rotation}.}\\ Reflection in line D maps foot 4 to foot 5.\\ Reflection in line C maps foot 5 to foot 6.\\ The combination of these 2 reflections is a rotation about the point of intersection of the two mirror lines by twice the angle between the mirror lines.

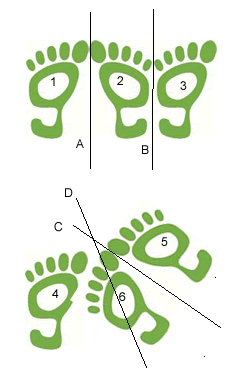
Consider the three reflections in the order they are given, performed on the foot shape at the far left. These three reflections give a glide reflection

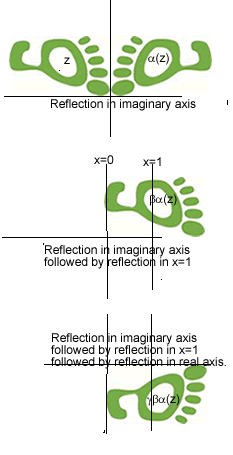
First the reflection $α (z) = - \bar{z}$ maps $z = x + iy$ to $- (x - iy) = - x + iy$ . This gives a reflection in the imaginary axis $x = 0$ resulting in a foot going toe-to-toe with the original, above the x-axis, with big toe near the origin, but pointing back in the opposite $(- x)$ direction.

Now perform the reflection in the axis $x = 1$ given by $β (z) = 2 - \bar{z}$ so that we have $β α (z)$ maps $z = x + iy$ to $- x + iy$ then to $2 - (- x - iy) = 2 + x + iy$ . This gives a foot pointing in the same direction as our original and immediately in front of it.

Now do the reflection in the axis y = 0 given by $γ (z) = \bar{z}$ so that the three reflections map $z = x + iy$ to $- x + iy$ then to $2 + x + iy$ then to $2 + x - iy .$ You end with a foot below the x-axis, pointing in the same direction as the original, with heel 2 units immediately in front of the toe of the original giving a combination of translation and reflection known as a glide reflection.

Repeating the reflections with the big toe of the new foot becoming the new origin each time gives the sequence of alternating feet walking left-to-right.