The isometries in the plane (reflections, rotations, translations and glide reflections) are transformations that preserve distances and angles.

Draw diagrams to show that all the isometries can be made up of combinations of reflections.

Complex numbers can be used to represent isometries. We write the conjugate of $z = x + iy$ as $\bar{z} = x - iy$ .

A reflection in the imaginary axis $x = 0$ is given by $α (z) = - \bar{z}$ . A reflection in the line $x = 1$ is given by $β (z) = 2 - \bar{z}$ . A reflection in the real axis $y = 0$ is given by $γ (z) = \bar{z}$ .

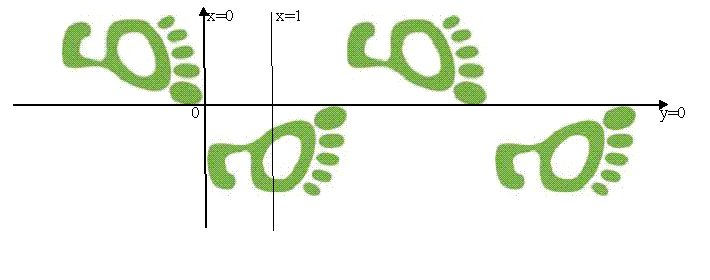
Find the formula for the transformation $γ β α (z)$ and explain how this transformation generates the footprint frieze pattern shown in the diagram.