Thank you to Lazarus from Colyton Grammar School and Andrei from Tudor Vianu National College, Bucharest for your solutions to this problem.We see that in all three cases the ratio XZ to XY is the Golden Ratio.
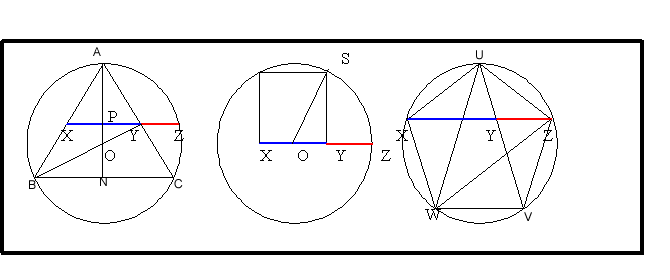
diagram
In the first diagram, taking the circle to have unit radius, AO = BO = CO = ZO.

Triangle BXO is similar to triangle XPO (angles 30o, 60o, 90o) so
BX = BOcos30 = Ö3
2

and XO = BOsin30 = 1/2, OP = XOsin30 = 1/4 and
XP = PY = XO cos30 = Ö3
4

so
XY = Ö3
2

.

Now consider triangle OPZ. Angle OPZ = 90o. Therefore using Pythagoras' Theorem,
PZ = Ö(1 - 1
16
 ) = Ö15
4

. So
XZ = XP + PZ = Ö3
4
 (1 + Ö5)

and
XZ
XY
 = 1
2
 (1 + Ö5)
which is the Golden Ratio.




In the second diagram, taking the side of the square XY as 1 unit and using Pythagoras Theorem for triangle OSY gives
OS= Ö5
2

which is the radius of the circle. So
OZ = Ö5
2

. Hence XZ = 1/2 (1 + Ö5) and
XZ
XY
 = 1
2
 (1 + Ö5)
again the Golden Ratio.




In the third diagram take the sides of the pentagon to be 1 unit long and the chords XZ and WZ etc. to be x units.

Triangles UXY, YVZ and XZW are similar isosceles triangles (angles of 36o, 72o and 72o) with VY = VZ = XY = 1 and YZ = x-1. We see that the ratio we want to find XZ/XY = x.

By similar triangles, taking the ratio of the long to the short sides, we get
x
1
= 1
x-1
which gives the quadratic equation
x2 - x - 1 = 0
with solutions 1/2(1 + Ö5) or 1/2(1 - Ö5). The latter is negative so does not make sense geometrically so the ratio must be the Golden Ratio:
1
2
 (1 + Ö5).