Description: Circles contain an equilateral triangle, a square and a pentagon. Find the ration of XZ to XY in each diagram.
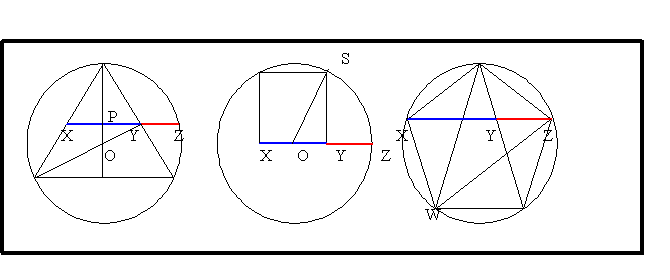golden solutions Taking the radius of the circle as 1 unit, in the equilateral triangle OY=1/2,
XP=PY= Ö3
4

and OP=1/4. Then, by Pythagoras Theorem,
PZ= Ö15
4
 .

So
XZ= Ö3
4
 (1 + Ö5).
Hence
XZ
XY
 = 1
2
 (1 + Ö5)
which is the golden ratio.

Taking the side of the square as one unit and using Pythagoras Theorem, the raduis of the circle is given by
OS = Ö5
2

. Hence XZ = 1/2(1 + Ö5) and
XZ
XY
 = 1
2
 (1 + Ö5)
which is the golden ratio again.

Take the side of the pentagon as one unit. Then XY=1 because it is in the isosceles triangle with angles 72o, 72o and 36o. Let the chord length XZ = x, then the ratio of the long to the short side in this triangle is
1
x-1

. The triangle XZW is similar and the ratio of the long to the short side is x/1. Hence we have
x
1
 = 1
x-1
which gives the quadratic equation
x2 -x -1 = 0
and, as x must be the positive root of this equation, this gives x = 1/2(1 + Ö5). Hence
XZ
XY
 = 1
2
 (1 + Ö5)
which is the golden ratio yet again. T