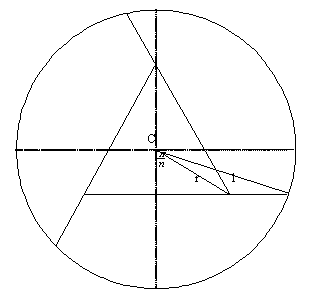
spokes The diagram shows the solution for 3 lines but the same principle applies to any regular polygon. For an n-gon the angle marked at the centre of the circle C will be
p
n

. As n gets larger the polygons will get smaller and the lines will 'radiate' out more like the spokes of a wheel.
For 3 lines, the area of each part must be
p
4

. Hence
p
4
 = 3
2
 r2 sin 2p
3
 = 3Ö3
4
 r2.
So
r =   æ
 ú
Ö
p
3Ö3
 
 = 0.7776
Let the polygon have sides of length x and the length of the line segments be L, then
x = 2rsin p
3
 = 1.3468.
Using Pythagoras Theorem
L = x
2
 +   æ
 ú
Ö
1 - r2cos2 p
3
 
 = 1.5947.
In general
rn2 = 2p
n(n+1)
 . 1
sin(2p/n)
 .
As
a
sina
 ® 1

as a ® ¥ we see that
rn ~   æ
 ú
Ö
1
n+1
 
 .

xn = 2rnsin p
n
and
Ln = xn
2
 +   æ
 ú
Ö
1 - (rncos p
n
 )2
 
where Ln ® 1 as n® ¥.

Here is an Octave program to do these calculations:

# divide disc into n+1 equal parts with n equal segments

# function y=s(n) y=sin(2*pi/n); endfunction

function y=t(n) y=tan(2*pi/n); endfunction

# function y=r(n) y=sqrt((2*pi)/(n*(n+1)*s(n))); endfunction

# function y=x(n) y=2*r(n)*sin(pi/n); endfunction

# function y=L(n)

z=pi*cot(pi/n);w=n*(n+1);

y=sin(pi/n)*r(n) + sqrt(1-(z/w));

endfunction

# disp(" ") disp("This gives [n,1/sqrt(n),r(n),x(n),L(n)]") disp(" ")

for n=(3:36) u=[n,1/sqrt(n),r(n),x(n),L(n)];disp(u) endfor

Here are the results for n = 3 to 36:

n 1/sqrt(n) r(n) x(n) L(n)
3 0.57735 0.77756 1.34677 1.59472
4 0.50000 0.56050 0.79267 1.31444
5 0.44721 0.46927 0.55166 1.20096
6 0.40825 0.41562 0.41562 1.14079
7 0.37796 0.37883 0.32873 1.10432
8 0.35355 0.35130 0.26888 1.08030
9 0.33333 0.32956 0.22543 1.06356
10 0.31623 0.31173 0.19266 1.05137
11 0.30151 0.29672 0.16719 1.04221
12 0.28868 0.28382 0.14692 1.03515
13 0.27735 0.27256 0.13045 1.02958
14 0.26726 0.26260 0.11687 1.02511
15
0.25820
0.25370 0.10550 1.02147
16 0.250000 0.245689 0.095863 1.018465
17 0.242536 0.238413 0.087617 1.015960
18 0.235702 0.231767 0.080492 1.013849
19 0.229416 0.225661 0.074285 1.012056
20 0.223607 0.220026 0.068839 1.010521
21 0.218218 0.214802 0.064029 1.009197
22 0.213201 0.209940 0.059755 1.008048
23 0.208514 0.205401 0.055937 1.007046
24 0.204124 0.201148 0.052510 1.006168
25 0.200000 0.197153 0.049420 1.005394
26 0.196116 0.193391 0.046621 1.004709
27 0.192450 0.189839 0.044078 1.004102
28 0.188982 0.186478 0.041758 1.003560
29 0.185695 0.183291 0.039634 1.003076
30 0.182574 0.180264 0.037685 1.002641
31 0.179605 0.177384 0.035891 1.002251
32 0.176777 0.174639 0.034235 1.001899
33 0.174078 0.172018 0.032703 1.001581
34 0.171499 0.169513 0.031281 1.001293
35 0.169031 0.167115 0.029960 1.001031
36 0.166667 0.164817 0.028730 1.000793