We received lots of solutions to this
problem.
Rebecca and Katherine from Stanley Park
Junior School, Emily from Durham Johnston Comprehensive School,
Jamie and James from Gillingham School, Fraser from Wallingford
School, Charlotte, Luke, Jordan, Stephen and Katie from Bosworth
College, Anna and James from Desford Community College, Henry
from Hitchin Boys' School, Gary from St Margaret's High School,
Peter from Fulford and Kayleigh,Rachel from Edwinstree Middle
School and Terence from Brumby Engineering College all got the
formula right and worked out which window had been incorrectly
priced. Well done all of you!
Here's what Fraser wrote:
The way to do it is first to find all the factors needed to work
out the formula. So there's Area and Perimeter. In fact some of
the shapes like shape A have an extra frame down the middle, so
we should call it 'length of the window frame'. If you work out
the area and add the perimeter, then add the perimeter again, you
will work out how much this window company charge for each
window. So
$A = \text{area}, P = \text{window frame length}, C =
\text{cost}$
$A + 2P = C$
So if you take example A for instance. It costs £88, its
window frame length is 28 and the area is 32.
32 + 28 + 28 = 88.
Gary and Peter told us that they drew
tables. For example, Peter says:
Make a table showing the perimeter (including the inside lines)
and area of each shape, and the cost of the windows. From this,
you can then see that the cost of the windows follows the general
formula of:
Cost = Area + (2 x Perimeter).
Some of you phrased your answer slightly
differently. For example, Jordan says:
Each line of frame costs £2, and each square of window costs
£1.
Can you see why this is the same as the
formula?
Here's what Anna and James told us about
the incorrectly priced window:
By applying our formula to all the shapes we found that the shape
that has been incorrectly priced was shape E. We can say this
because the perimeter of the shape is 18 and the area of the
shape is 12. When we put this into our formula we get Price = 12
+ (2 x 18) which should equal 55 if the price is correct. However
the price is incorrect as the formula shows that the price should
be £48, therefore window E has been incorrectly
priced.
Katie noticed something else about window
E.
Also because the area of the pane of glass is even and so is
twice the length of the frame (because you've multiplied it by
two you can divide it by two so it is even) then the cost for the
window must be even also (even + even = even). £55 is not
even so this also means that it is wrong.
Well spotted!
Terence used simultaneous equations to
find the formula, and checked it (and found the window with the
wrong price) using a spreadsheet.
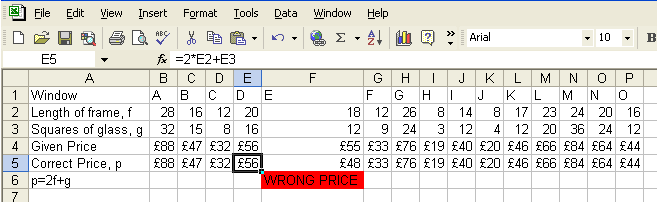
f is how many units of frame there are, and g is how many units of glass
there are.
I found the formula by using simultaneous equations: Window C has 12 units of frame, 8 units of glass, and costs £32. So
12f+8g=32. (Equation 1) Window F also has 12 units of frame, but has 9 units of glass and costs
£33. So 12f+9g=33. (Equation 2) So by doing (Equation 2)-(Equation 1), I get: 12f-12f+9g-8g=33-32, which
simplifies into: g=1 So, I put 1 instead of g in Equation 1 to get: 12f+8=32, so 12f=24 and
f=2, which gives the formula for the cost of a window as c=2f+g.
Window E is incorrectly priced, because it has 18 units of frame and 12
units of glass.
So, the price should be (18x2)+12 = £48.
Instead, it is shown as £55, £7 more! You can see this in my spreadsheet.