Many people suggested the answer should
be 6 by 8, because this is "double" the 6 by 4 example given in
the problem. However, this doesn't take into account squares like
the red ones below:
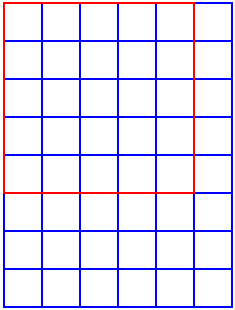
In the first picture, we have a 5 x 5
square. You cannot fit any of these in a 6 x 4 rectangle, but you
can fit them in a 6 x 8 rectangle.
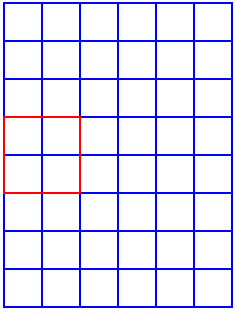
Imagine the 6 x 8 rectangle is made up
from joining two 6 x 4 rectangles. In the second picture, you can
see a 2 x 2 square. Where the 6 x 4 rectangles meet there will be
an extra row of these 2 x 2 squares that would not be in either
of the 6 x 4 rectangles.
One way to approach this problem is to
try some examples and set your working out in a table, and then
look for patterns and try to explain them. Sam from OPGS sent
us his table:
|
columns:
rows:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
2 |
5 |
8 |
11 |
14 |
17 |
20 |
|
3 |
3 |
8 |
14 |
20 |
26 |
32 |
38 |
|
4 |
4 |
11 |
20 |
30 |
40 |
50 |
60 |
|
5 |
5 |
14 |
26 |
40 |
55 |
70 |
85 |
|
6 |
6 |
17 |
32 |
50 |
70 |
91 |
112 |
| 7 |
7 |
20 |
38 |
60 |
85 |
112 |
140 |
Since the number of squares in an n x m
rectangle is the same as the number of squares in an m x n
rectangle, we will look only at rectangles with at least as many
columns as rows. These are italicised in the above table.
First we notice that, if there is one
row, increasing the number of columns by one increases the number
of squares by 1. This is because the only size of square that we
can make is 1x 1, so adding a column adds just one square.
If there are two rows, adding an extra
column increases the number of squares by 3. Why is this? Well,
if we add an extra column we can make 2 additional 1 x 1 squares
and 1 additional 2 x 2 square. This is a total of three extra
squares. If we continue the pattern 2, 5, 8, ... in the 2 row, we
eventually get to ..., 98, 101, .... - missing out 100. This
tells us that it isn't possible to make a rectangle with 100
squares which has 2 rows.
If there are three rows, adding an extra
column allows us to make 3 more 1 x 1 squares, 2 more 2 x 2
squares and 1 more 3 x 3 square. This is a total of 6 = 3 + 2 + 1
squares. This gives us the sequence 14, 20, 26, 32, ... 98, 104,
... which tells us that we can't make a rectangle with exactly
100 squares which has 3 rows.
Using the same reasoning for four rows,
we see adding a column increases the number of squares by 10, and
that we can make rectangles with 20, 30, ..., 90, 100, 110, ...
squares. 100 is in this list! In fact, a 4x 11 rectangle contains
exactly 100 squares.
We can repeat this for the other rows in
the table to find all the rectangles with exactly 100 squares.
These are 1 x 100, 4 x 11 and 5 x 8.
Sandeep from Nrayana Junior College and
Terence from Brumby Engineering College used a slightly different
approach to count the number of squares in rectangles of
different sizes, starting with the examples from the problem
page. Here is Sandeep's method:
In a 2 ×3 rectangle, squares of side 1 unit and squares of side 2
units can be formed. Number of squares of side 1 unit is 2 ×3 = 6.
Number of squares of side 2 units is 1 ×2 = 2.
Therefore the total number of squares in a 2 ×3 rectangle is
6 + 2 = 8.
Similarly if we consider a 3×4 rectangle there are a total of
20 squares. Number of squares of side 1 unit: 3 ×4 = 12.
Number of squares of side 2 units: 2 ×3 = (3-1) ×(4-1) = 6.
Number of squares of side 3 units: 1 ×2 = (3-2) ×(4-2) = 2.
Total number of squares = 12 + 6 + 2 = 20.
We can generalise this fact by taking a rectangle of x rows and y columns:
Total number of squares = x ×y + (x-1) ×(y-1) + (x-2) ×(y-2) + ¼.
The addition series stops only when either the rows or the columns reduces to
1.
By trial and error, 5 ×8 and 4 ×11
rectangles contain exactly 100 squares. There can be no other rectangles
containing 100 squares. This can be verified by increasing or decreasing
the number of rows and columns.

