The Von Koch curve is a fractal. The rule for generating this
curve is to start with an equilateral triangle and to replace
each line segment by a zig-zag curve (a generator) made up of
$4$ copies of the line segment it replaces, each reduced to one
third of the original length.
Click on the red button below to see the first six stages of
the infinite process for generating the Von Koch curve.
This text is usually replaced by the Flash movie.
TThe original equilateral triangle has side 1 unit. Work out the length
of this curve in the first few stages and the length of the fractal curve
formed when the process goes on indefinitely.
Now suppose you made a poster for your classroom with coloured paper by
drawing an equilateral triangle for Stage 0 and then cutting smaller
equilateral triangles and sticking them on the edge. What is the total area
of all the triangles you would stick on one edge if you could continue
the process indefinitely to make the Von Koch curve?
So what is the area inside the Von Koch curve?
Find the dimension of the Von Koch curve using the formula n=md,
where where n is the number of self similar pieces in the generator
and m is the magnification factor.
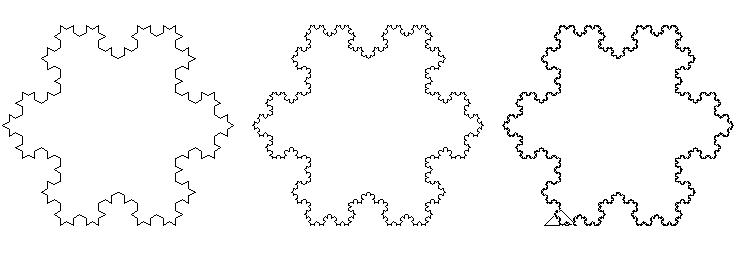
The diagrams below show Stages 0 to 5 in the evolution of the
Von Koch curve. The Logo program for drawing this fractal is given
in the Notes.
See
First Forward for a ten part series giving an introduction to
Logo programming for beginners.