Andre from Tudor Vianu National College, Bucharest, Romania and Shaun from Nottingham High School both sent in excellent solutons to this problem.

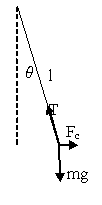
After drawing the picture, I observed that the forces

(the gravitational force acting on the ball, the tension in the wire and the

centrifugal force) keep the body in equilibrium. Considering the

centrifugal force, I work in a non-inertial frame of reference,

i.e. in the frame centred on the ball, which is in an

accelerated movement in respect to Earth.

In terms of the vectors we have

m \bar{g} + {\bar{F}}_{c} + \bar{T} = 0 .

Resolving horizontally and vertically and using F=ma (where

a

is the acceleration towards the centre and

T

is the magnitude of the tension in the string):

T \cos θ = mg

T \sin θ = ml \sin θ ω^{2}

Eliminating

T

l ω^{2} \cos θ = g

and hence the angle

θ

\cos^{- 1} \frac{g}{l ω^{2}}

I know that $\cos^{- 1}$ is a decreasing function in the interval of interest for the problem. As $ω$ increases, the angle $θ$ also increases and the whirling ball rises up, the radius of its circular path also increasing.

The ball can whirl in a circle while $θ > 0$ . So, as I explained above, to find the smallest angular velocity, I have to find the smallest angle. For $θ \to 0$ , $\frac{g}{l ω^{2}} \to 1$ and so

$ω \to \sqrt{\frac{g}{l}} .$

This is the smallest angular velocity with which the ball could rotate in a circle.

The period of this movement is:

$T = \frac{2 π}{ω} = 2 π \sqrt{\frac{l}{g}} .$

It is interesting to observe that this is also the period of isochronal oscillations of the mathematical pendulum, i.e. the period of oscillation of a material point of mass $m$ attached to an inextensible string without mass deviated from the vertical by angles less than $5^{o}$ .