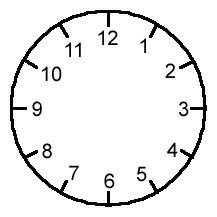
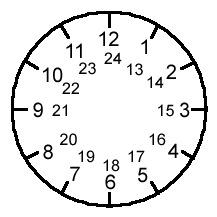
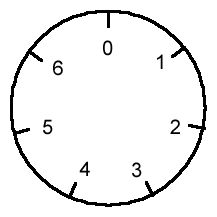
The best way to introduce modular arithmetic is to think of the face of a
clock.
The numbers go from 1 to 12, but when you get to ``13 o'clock'', it actually
becomes 1 o'clock again (think of how the 24 hour clock numbering works). So
13 becomes 1, 14 becomes 2, and so on. This can keep going, so when you get
to ``25 o'clock'', you are actually back round to where 1 o'clock is on the
clock face (and also where 13 o'clock was too).
So in this clock world, you only care where you are in relation to the numbers
1 to 12. In this world, 1, 13, 25, 37, ¼ are all thought of as the
same thing, as are 2, 14, 26, 38, ¼ and so on.
What we are saying is ``13=1+some multiple of 12'', and ``38=2+some
multiple of 12'', or, alternatively, ``the remainder when you divide 13 by 12
is 1'' and ``the remainder when you divide 38 by 12 is 2''. The way we write
this mathematically is 13 º 1 mod 12, 38 º 2 mod 12, and so on.
This is read as ``13 is congruent to 1 mod (or modulo) 12'' and ``38 is
congruent to 2 mod 12''.
But you don't have to work only in mod 12 (that's the technical term for it).
For example, you could work mod 7, or mod 46 instead if you wanted to (just
think of clocks numbered from 1 to 7 and 1 to 46 respectively; every time you
get past the biggest number, you reset to 1 again).
Let's go back to the normal clock face with the numbers 1 to 12 on it for a
moment. Mathematicians usually prefer to put a 0 where the 12 would normally
be, so that you would usually write (for example) 24 º 0 mod 12 rather
than 24 º 12 mod 12, although both of these are correct. That is, we
think of a normal clock face as being numbered from 0 to 11 instead. This
makes sense: we'd normally say that 24 leaves a remainder of 0 when we divide
by 12, rather than saying it leaves a remainder of 12 when we divide by 12!
Let's be a bit more formal. In general, if you are working mod n (where n
is any whole number), we write a º b mod n if a and b leave the same
remainder when you divide them by n. This is the same as saying that we
write a º b mod n if n divides a-b. (Look at what we did earlier to
see that this definition fits with our examples above.) So far, we've only talked about notation. Now let's do some maths, and see
how congruences (what we've described above) can make things a bit clearer. Here are some useful properties. We can add congruences. That is, if
a º b mod n and c º d mod n, then a+c º b+d mod n. Why is
this? Well, a º b mod n means that a=b+k n, where k is an integer.
Similarly, c º d mod n means that c=d+l n, where l is an integer. So
a+c=(b+k n)+(d+l n)=(b+d)+(k+l)n, so a+c º b+d mod n. For example,
17 º 4 mod 13, and 42 º 3mod 13, so
17+42 º 4+3 º 7mod 13. Note that both of the congruences that we're
adding are mod n, and so is the answer - we don't add the moduli.
Now you prove that if a º b mod n and c º d mod n then
a-c º b-d mod n. Also, prove that we can do something similar for
multiplication: if a º b mod n and c º d mod n, then
a c º b d mod n. You can prove this in the same way that we used above for
addition. Again, both of the congruences that we're multiplying are mod n,
and so is the answer - we don't multiply the moduli. Can you come up with
an example to disprove the claim that a º b mod n and
c º d mod m means that a c º b d mod m n?
Division is a bit more tricky: you have to be really careful. Here's an
example of why. 10 º 2 mod 8. But if we ``divide both sides by 2'',
we'd have 5 º 1 mod 8, which is clearly nonsense! To get a true
congruence, we'd have to divide the 8 by 2 as well: 5 º 1 mod 4 is fine.
Why? Well, a º b mod n means that a=b+k n for some integer n. But
now this is a normal equation, and if we're going to divide a by something,
then we have to divide all of the right-hand side by 2 as well,
including k n. In general, it's best not to divide congruences; instead,
think about what they really mean (rather than using the shorthand) and work
from there.
Things are quite special if we work mod p, where p is prime, because then
each number that isn't 0 mod p has what we call an inverse (or a
multiplicative inverse, if we're being fancy). What that means is that
for each a\not º 0 mod p, there is a b such that a b º 1 mod p.
Let's think about an example. We'll work mod 7. Then really the only non-zero
things are 1, 2, 3, 4, 5 and 6 (because every other whole number is equivalent
to one of them or 0). So let's find inverses for them. Well, 1 is pretty
easy: 1×1 º 1 mod 7. What about 2? 2×4 º 1 mod 7.
So 4 is the inverse of 2. In fact, we can also see from this that 2 is the
inverse of 4 - so that's saved us some work! 3×5 º 1 mod 7, so
3 and 5 are inverses. And finally, 6×6 º 1 mod 7, so 6 is the
inverse of itself. So yes, each of the non-zero elements mod 7 has an inverse.
Try some primes out yourself: 11 and 13 are fairly small! If you're feeling
confident, see whether you can discover which numbers have inverses mod 4, or
mod 6, or mod 8. What about mod 15? Do you notice any patterns?
To prove this, things are going to get a tiny bit more tricky, so I'm going to
save the proof for the end and first give an example of using
congruences to do useful mathematics.
Suppose we're given the number 11111111 and someone asks us whether it's
divisible by 3. We could try to actually divide it. But you probably know a
much easier method: we add up the digits and see whether that's divisible by 3.
There's a whole article about this sort of divisibility test
here.
Let's prove this using congruence notation. Suppose that our number is
an 10n+an-110n-1+¼+10a1+a0, so it looks like
an an-1¼a1 a0. Then the sum of its digits is
an+an-1+¼+a1+a0. We'd like to prove that
an10n+an-110n-1+¼+10a1+a0 is divisible by 3 if and only if
an+an-1+¼+a1+a0 is divisible by 3. Now we notice that
10 º 1 mod 3, so 10×10 º 1 mod 3, and more generally
10k º 1 mod 3 for all k. Using our results from earlier about adding
and multiplying congruences, we discover
|
an10n+an-110n-1+¼+10a1+a0 º an+an-1+¼+a1+a0 mod 3 |
|
So if our number is divisible by 3 (that is, if
an10n+an-110n-1+¼+10a1+a0 º 0 mod 3), then certainly so
is the sum of its digits, and vice versa, as we wanted! The congruence
notation hasn't really done any of the maths for us, but it's hopefully made
it a bit easier to write out the proof clearly. See whether you can use the
notation to prove any of the other divisibility tests in that article.
Now for the proof I promised you earlier. We're going to show that if a and
n have no common factors, then a has a multiplicative inverse mod n
(reminder: that means a number b such that a×b º 1 mod n). In
particular, if n is prime, then its only factor apart from 1 is itself, so
saying ``a and n share no common factors'' is just the same as saying
``a isn't divisible by n'', that is, a\not º 0 mod p: this is what
we had above. I'm going to assume that you know about using Euclid's
algorithm to solve equations of the form a x+b y=1 where a and b have no
common factors. There's a really good article explaining this
here, so
have a read, and then come back.
If you're reading this far, then hopefully you'll agree that if a and n
share no common factors, then we can find x and y such that a x+n y=1.
(The fancy name for this is Bézout's Theorem.) So we've got our x
and y such that a x+n y=1. We can rewrite this as a x=1-y n, and now let's
use the congruence notation from earlier: we have a x º 1 mod n. So now
x is the multiplicative inverse of a mod n, and we're done!
Here's a challenge: use this technique based on Euclid's algorithm to find the
inverse of 14 mod 37.
Understanding this is the beginning of a branch of mathematics called Number
Theory, which contains some beautiful, fascinating and amazing theorems.
Enjoy!
This article is based on a
contribution to Ask NRICH by Matthew Buckley.