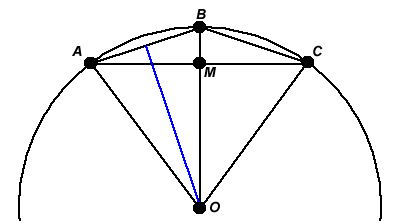
Chris from Saint John Payne School sent
in clear diagrams to explain the first part.
Diana thought about a general result.
Here's what she sent us.
In general, suppose that we've placed points
,
and
in such a
way that
. I'm going to show that
. This is called a double angle
formula.
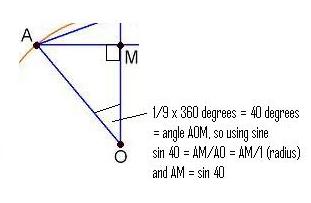
From triangle
, we know that
(as the circle
has radius
).
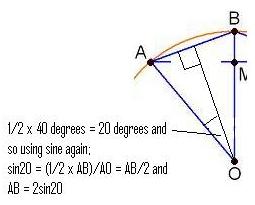
From triangle
, we know that
(the blue line
bisects the angle at
and since triangle
is isosceles, the blue
line meets
at a right angle, so we can think about two right-angled
triangles, each with angle
at
).
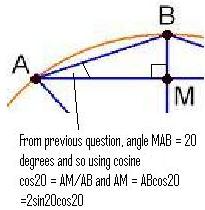
Since
(from the isosceles triangle
),
we know that
, and so from triangle
we see
that
.
Putting together the last two paragraphs, we get
. But also
, so
.