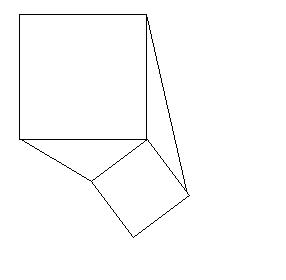
Draw any two squares which meet at a common vertex

C

and join the adjacent vertices to make two triangles

CAB

and

CDE

Construct the perpendicular from $C$ to $AB$ , (the altitude of the triangle). When you extend this line where does it cut $DE$ ?

Now bisect the line $AB$ to find the midpoint of this line $M$ . Draw the median $MC$ of triangle $ABC$ and extend it to cut $DE$ . What do you notice about the lines $MC$ and $DE$ ?

Will you get the same results about the two triangles formed if you draw squares of different sizes or at different angles to each other? Make a conjecture about the altitude of one of these triangles and prove your conjecture.

Thank you Geoff Faux for suggesting this problem.