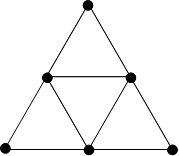
This network has nine edges which meet at six nodes. The numbers
1, 2, 3, 4, 5, 6 are placed at the nodes, with a different number
at each node. Is it possible to do this so that the sum of the
two numbers at the ends of an edge is different for each edge?
Either show a way of doing this, or prove that it is
impossible.
This problem is taken from the UKMT Junior Mathematical Olympiad.